
分析 (1)①-②×3得出-17y=51,求出y,把y的值代入①求出x即可;
(2)先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:(1)$\left\{\begin{array}{l}{3x-5y=6①}\\{x+4y=-15②}\end{array}\right.$
①-②×3得:-17y=51,
解得:y=-3,
把y=-3代入①得:3x+15=6,
解得:x=-3,
所以原方程组的解为:$\left\{\begin{array}{l}{x=-3}\\{y=-3}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{3x>x-2①}\\{\frac{x+1}{3}>2x②}\end{array}\right.$
∵解不等式①得:x>-1,
解不等式②得:x<$\frac{1}{5}$,
∴不等式组的解集为-1<x<$\frac{1}{5}$.
点评 本题考查了解二元一次方程组和解一元一次不等式组的应用,能把二元一次方程组转化成一元一次方程是解(1)的关键,能根据不等式的解集找出不等式组的解集是解(2)的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
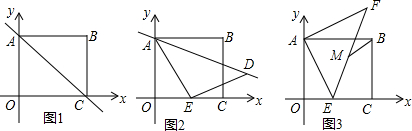
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 平均分(分) | 中位数(分) | 众数(分) | |
| 初中部 | 85 | 85 | 85 |
| 高中部 | 85 | 80 | 100 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 候选人 | 测试成绩(百分制) | |
| 笔试 | 面试 | |
| 甲 | 95 | 85 |
| 乙 | 83 | 95 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这个函数的图象位于第二、第四象限 | |
| B. | 当x>0时,y随x的增大而增大 | |
| C. | 这个函数的图象既是轴对称图形又是中心对称图形 | |
| D. | 当x<0时,y随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
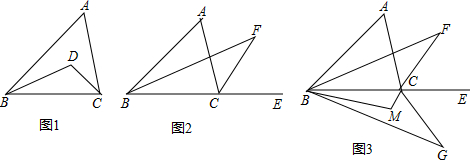
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com