
综合与探究:如图,在平面直角坐标系中,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点 D是该抛物线的顶点.
D是该抛物线的顶点.
(1)求直线AC的解析式及B、D两点的坐标;
(2)点P是x轴上一个动点,过P作直线l∥AC交抛物线于点Q.试探究:随着P点的运动,在抛物线上是否存在点Q,使以点A、P、Q、C为顶点的四边形是平行四边形,若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由;
(3 )请在直线AC上找一点M,使△BDM的周长最小,求出M点的坐标.
)请在直线AC上找一点M,使△BDM的周长最小,求出M点的坐标.
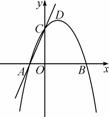
解:(1)当y=0时,-x2+2x+3=0,解得x1=-1,x2=3.
∵点A在点B的左侧,∴A、B的坐标分别是(-1,0)、(3,0).(2分)
当x=0时,y=3,∴C点的坐标为(0,3).
设直线AC的解析式为y=k1x+b1(k1≠0),则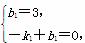
解得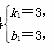 ∴直线AC的解析式为y=3x+3,(4分)
∴直线AC的解析式为y=3x+3,(4分)
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点D的坐标为(1,4).(6分)
(2)抛物线上有三个这样的点Q,分别为Q1(2,3),Q2(1+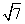 ,-3),Q3(1-
,-3),Q3(1-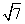 ,-3).(9分)
,-3).(9分)
(3)过点B作BB′⊥AC于点F,使B′F=BF,则B为点B关于直 线AC的对称点,连接BD交直线于AC于点M,则点M为所求.
线AC的对称点,连接BD交直线于AC于点M,则点M为所求.
过点B′作B′E⊥x轴于点E.(10分)
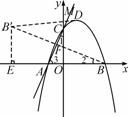
∵∠1和∠2都是∠3的余角,
∴∠1=∠2.
Rt△AOC∽Rt△AFB,
∴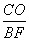 =
=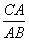 ,
,
由A(-1,0),B(3,0),C(0,3)得
OA=1,OB=3,
∴AC=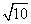 ,AB=4,
,AB=4,
∴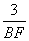 =
=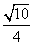 ,∴BF=
,∴BF=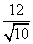 ,
,
∴BB′=2BF=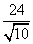 .由∠1=∠2可得Rt△
.由∠1=∠2可得Rt△ AOC∽R
AOC∽R t△B′EB,
t△B′EB,
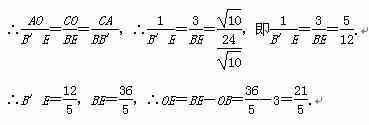 ∴B′点的坐标为
∴B′点的坐标为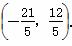
设直线B′D的解析式为y=k2x+b2(k2≠0)
∴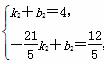 解得
解得 ∴y=
∴y=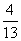 x+
x+ .
.
由 解得
解得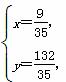 ∴M点的坐标为
∴M点的坐标为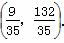


科目:初中数学 来源: 题型:
王红和刘芳两人在玩转盘游戏,如图7,把转盘甲、乙分别分成3等份,并在每一份内标上数字,游戏规则是:转动两个转盘,停止后,指针所指的两个数字之和为7时,王红胜;数字之和为8时,刘芳胜.那么这二人中获胜可能性较大的是_______.
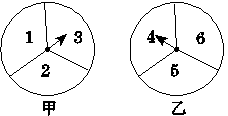
图7
查看答案和解析>>
科目:初中数学 来源: 题型:
有三张正面分别写有数-2 ,-1,1的卡片,它们的背面完全相同,将这三张卡片背面朝上洗匀后随机抽取一张,以其正面的数作为x的值,放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面的数作为y的值,两次结果记为(x,y).
(1)用画树状图法或列表法表示(x,y)所有可能出现的结果;
(2)求使代数式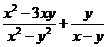 有意义的(x,y)出现的概率;
有意义的(x,y)出现的概率;
(3)化简代数式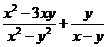 ,并求使代数式的值为整数的(x,y)出现的概率.
,并求使代数式的值为整数的(x,y)出现的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
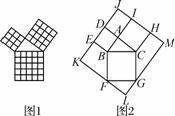
勾股定理是几何中的一个重要定理, 在我国古算书《周髀算经》中就有“若勾三,股四,则弦五
在我国古算书《周髀算经》中就有“若勾三,股四,则弦五 ”的记载,如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积验证勾股定理,图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
”的记载,如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积验证勾股定理,图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
A.90 B.100 C.110 D.121
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)如图1,若O点是∠ABC与∠ACB的平分线的交点;
(2)如图2,若O点是外角∠DBC与∠ECB的平分线的交点;
(3)如图3,若O点是∠ABC与外角∠ACD的平分线的交点,试探索下列各图中∠BOC与∠A的关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com