
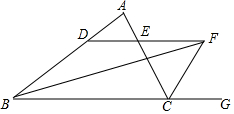
 如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=8cm,DE=3cm,求CE的长.
如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=8cm,DE=3cm,求CE的长.  浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
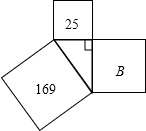 如图所示.以直角三角形的三条边为边长分别作正方形.依据图中所给条件,回答下列问题:
如图所示.以直角三角形的三条边为边长分别作正方形.依据图中所给条件,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
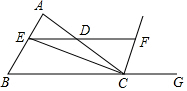 如图所示,CE为△ABC中∠BCA的角平分线,过E作BC的平行线交AC于点D,交∠ACG的平分线于点F,探究DE与DF之间的关系,并说明理由.
如图所示,CE为△ABC中∠BCA的角平分线,过E作BC的平行线交AC于点D,交∠ACG的平分线于点F,探究DE与DF之间的关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小明家(点P)与限速60千米/小时的高速公路AB之间有一块巨型广告牌CD,已知小明家距离高速公路60米,在△ABP中,∠A=60°,∠B=45°,一辆车自西向东匀速行驶,小明从P处观察,看到它在A处消失9秒后又在B处出现,请问这辆车经过AB段是否超速?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,小明家(点P)与限速60千米/小时的高速公路AB之间有一块巨型广告牌CD,已知小明家距离高速公路60米,在△ABP中,∠A=60°,∠B=45°,一辆车自西向东匀速行驶,小明从P处观察,看到它在A处消失9秒后又在B处出现,请问这辆车经过AB段是否超速?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com