
【题目】如图,已知关于x的二次函数y=x2+mx的图象经过原点O,并且与x轴交于点A,对称轴为直线x=1. 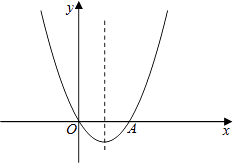
(1)常数m= , 点A的坐标为;
(2)若关于x的一元二次方程x2+mx=n(n为常数)有两个不相等的实数根,求n的取值范围;
(3)若关于x的一元二次方程x2+mx﹣k=0(k为常数)在﹣2<x<3的范围内有解,求k的取值范围.
【答案】
(1)-2;(2,0)
(2)解:∵一元二次方程x2﹣2x=n有两个不相等的实数根,
∴△=4+4n>0,
n>﹣1
(3)解:一元二次方程x2﹣2x﹣k=0有解,
则△=4+4k≥0,
k≥﹣1,
方程的解为:x=1± ![]() ,
,
∵方程在﹣2<x<3的范围内有解,
1﹣ ![]() >﹣2,k<8,
>﹣2,k<8,
1+ ![]() <3,k<3,
<3,k<3,
∴﹣1≤k<8
【解析】解:(1)∵对称轴为直线x=1, ∴﹣ ![]() =1,m=﹣2,
=1,m=﹣2,
则二次函数解析式为y=x2﹣2x,
x2﹣2x=0,x=0或2,
∴点A的坐标为 (2,0),
∴常数m=﹣2,点A的坐标为 (2,0);
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


科目:初中数学 来源: 题型:
【题目】已知在数轴l上,一动点Q从原点O出发,沿直线l以每秒钟2个单位长度的速度来回移动,其移动方式是先向右移动1个单位长度,再向左移动2个单位长度,又向右移动3个单位长度,再向左移动4个单位长度,又向右移动5个单位长度…
![]()
(1)求出5秒钟后动点Q所处的位置;
(2)如果在数轴l上还有一个定点A,且A与原点O相距20个单位长度,问:动点Q从原点出发,可能与点A重合吗?若能,则第一次与点A重合需多长时间?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细观察下面由“※”组成的图案和算式,解答问题:
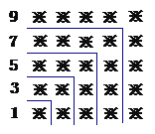
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)请计算:
1+3+5+7+9+ … +19= ;
(2)请猜想:
1+3+5+7+9+ … +(2n-1)+(2n+1)+(2n+3)= ;
(3)请用上述规律计算:
103+105+107+ … +2013+2015
查看答案和解析>>
科目:初中数学 来源: 题型:
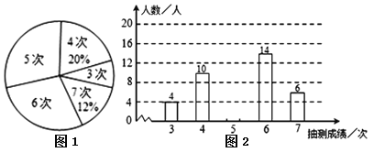
【题目】为了解某校八年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成图1和图2两幅尚不完整的统计图.
(1)本次抽测的男生有 人,抽测成绩的众数是 ;
(2)请你将图2的统计图补充完整;
(3)若规定引体向上5次以上(含5次)为体能达标,则该校400名八年级男生中估计有多少人体能达标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面各小题括号里的数,均是它前面的方程的解的是( )
A. 3x﹣1=5(2) B. ![]() +1=0(﹣5,﹣7)
+1=0(﹣5,﹣7)
C. x2﹣3x=4(4,1) D. x(x﹣2)(x+4)=0(2,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图正方形ABCD的边长为2,点E、F、G、H分别在AD、AB、BC、CD上的点,且AE=BF=CG=DH,分别将△AEF、△BFG、△CGH、△DHE沿EF、FG、GH、HE翻折,得四边形MNKP,设AE=x,S四边形MNKP=y,则y关于x的函数图象大致为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠B=90°,∠C=30°,点D从C点出发沿着CA方向以2个单位每秒的速度向终点A运动,同时点E从点A出发沿AB方向以1个单位每秒的速度向终点B运动。设点D,E的运动时间为t秒,DF⊥BC于F
(1)求证:AE=DF;
(2)如图2,连接EF,![]()
①是否存在t,使得四边形AEFD为菱形?若存在,求出t的值;若不存在,请说明理由
②连接DE,当△DEF是直角三角形时,求t的值
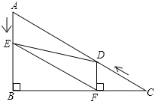
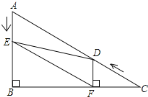

图1 图2 备用图 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,∠C=90°,AC=BC,直线m经过点C,分别过点A,B作直线m的垂线,垂足分别为点E,F,若AE=3,AC=5,则线段EF的长为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com