
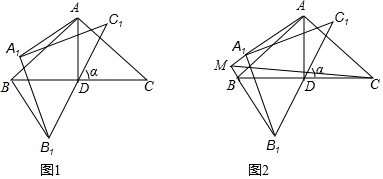
分析 (1)结论:AA1=BB1,且AA1⊥BB1.如图1中,延长AA1交B1B于M.连接AB1.由DA=DB=DC=DA1=DB1=DC1,推出A、A1、B、B1、C共圆,推出∠MAB1=$\frac{1}{2}$∠A1DB1=45°,∠MBA1=$\frac{1}{2}$∠ADB=45°,推出∠AMB1=90°,由∠ADA1=∠BDB1,推出$\widehat{A{A}_{1}}$=$\widehat{B{B}_{1}}$,推出AA1=BB1,延长即可证明.
(2)由(1)可知∠AMB=90°,推出点M在以AB为直径的圆上,推出当CM经过线段AB中点时,可得CM的最大值以及最小值CM′.
解答 解:(1)结论:AA1=BB1,且AA1⊥BB1.
理由:如图1中,延长AA1交B1B于M.连接AB1.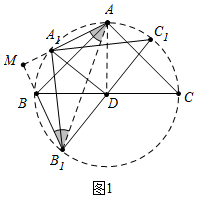
∵AB=AC,DB=DC,∠BAC=90°,
∴DA=DB=DC=DA1=DB1=DC1,
∴A、A1、B、B1、C共圆,
∴∠MAB1=$\frac{1}{2}$∠A1DB1=45°,∠MBA1=$\frac{1}{2}$∠ADB=45°,
∴∠AMB1=90°,
∵∠ADA1=∠BDB1,
∴$\widehat{A{A}_{1}}$=$\widehat{B{B}_{1}}$,
∴AA1=BB1,
∴AA1=BB1,且AA1⊥BB1.
(2)如图2中,
由(1)可知∠AMB=90°,
∴点M在以AB为直径的圆上,
∴当CM经过线段AB中点时,可得CM的最大值以及最小值CM′,
在Rt△AOC中,OC=$\sqrt{O{A}^{2}+A{C}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∵OM=OM′=1,
∴OM的最大值为$\sqrt{5}$+1,OM的最小值为$\sqrt{5}$-1,
∴$\sqrt{5}$-1≤OM≤$\sqrt{5}$+1.
点评 本题考查旋转变换、等腰直角三角形的性质、圆的有关知识,解题的关键是利用辅助圆解决问题,属于中考压轴题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
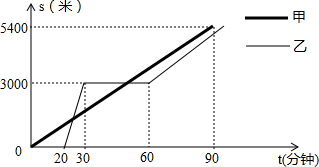 某景区的三个景点A,B,C在同一线路上,甲,乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C,甲,乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据信息回答下列问题:
某景区的三个景点A,B,C在同一线路上,甲,乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C,甲,乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |
| B. |
| ||||||||||||||||||||||||||
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若AC⊥BD,则?ABCD是正方形 | B. | 若AC=BD,则?ABCD是正方形 | ||
| C. | 若AB⊥BC,则?ABCD是菱形 | D. | 若AB=BC,则?ABCD是菱形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com