
【题目】某农场学校积极开展阳光体育活动,组织了九年级学生定点投篮,规定每人投篮3次.现对九年级(1)班每名学生投中的次数进行统计,绘制成如下的两幅统计图,根据图中提供的信息,回答下列问题.
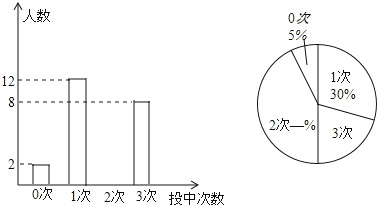
(1)求出九年级(1)班学生人数;
(2)补全两个统计图;
(3)求出扇形统计图中3次的圆心角的度数;
(4)若九年级有学生200人,估计投中次数在2次以上(包括2次)的人数.
【答案】解:(1)九年级(1)班学生人数:2÷5%=40(人)。
(2)投中2次的人数:40﹣2﹣12﹣8=18(人),
投中2次的百分比18÷40×100%=45%,投中3次的百分比8÷40×100%=20%。
补全两个统计图如图所示:
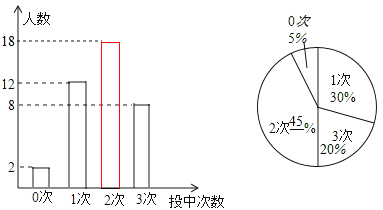
(3)扇形统计图中3次的圆心角的度数为360°×20%=72°。
(4)200×(1﹣5%﹣30%)=130(人),
答:投中次数在2次以上(包括2次)的人数有130人。
【解析】
试题(1)根据总数=频数÷百分比进行计算即可。
(2)利用总数减去投中0次,1次,3次的人数可得投中2次的人数,再根据百分比=频数÷总数×100%可得投中2次、3次的百分比,再补全图形即可。
(3)图中3次的圆心角的度数=360°×投中3次的百分比。
(4)根据样本估计总体的方法进行计算即可。


科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠C=90°,O是AB的中点,AC=6,∠MON=90°,将∠MON绕点O旋转,OM、ON分别交边AC于点D,交边BC于点E(D、E不与A、B、C重合)
(1)判断△ODE的形状,并说明理由;
(2)在旋转过程中,四边形CDOE的面积是否发生变化?若不改变,直接写出这个值,若改变,请说明理由;
(3)如图2,DE的中点为G,CG的延长线交AB于F,请直接写出四边形CDFE的面积S的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
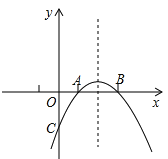
【题目】已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).
(1)求抛物线的解析式;
(2)设点P在该抛物线上滑动,且满足条件S△PAB=1的点P有几个?并求出所有点P的坐标;
(3)设抛物线交y轴于点C,问该抛物线对称轴上是否存在点M,使得△MAC的周长最小?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
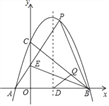
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C(0,4).
(1)求此抛物线的解析式;
(2)设点P(2,n)在此抛物线上,AP交y轴于点E,连接BE,BP,请判断△BEP的形状,并说明理由;
(3)设抛物线的对称轴交x轴于点D,在线段BC上是否存在点Q,使得△DBQ成为等腰直角三角形?若存在,求出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A,B两点的俯角分别为30°,45°,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
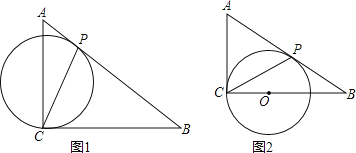
【题目】如图1,Rt△ACB中,AC=3,BC=4,有一动圆⊙O始终与Rt△ACB的斜边AB相切于动点P,且⊙O始终经过直角顶点C.
(1)如图2,当⊙O 运动至与直角边AC相切时,求此时⊙O 的半径r的长;
(2)试求⊙O 的半径r的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
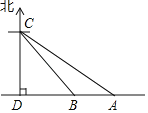
【题目】据调查,超速行驶是引发交通事故的主要原因之一.小强用所学知识对一条笔直公路上的车辆进行测速,如图所示,观测点C到公路的距离CD=200m,检测路段的起点A位于点C的南偏东60°方向上,终点B位于点C的南偏东45°方向上.一辆轿车由东向西匀速行驶,测得此车由A处行驶到B处的时间为10s.问此车是否超过了该路段16m/s的限制速度?(观测点C离地面的距离忽略不计,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com