
分析 (1)不降价时,利润=不降价时商品的单件利润×商品的件数.
(2)①可根据:降价后的单件利润×降价后销售的商品的件数=2090,来列出方程,求出未知数的值,
②首先得出y与x的函数关系,利用二次函数最值求法得出答案.
解答 解:(1)若商店经营该商品不降价,则一天可获利润:100×(100-80)=2000(元);
故答案为:2000;
(2)①设该商品每件降价x元,依题意,得
(100-80-x)(100+10x)=2090,
即x2-10x+9=0.
解得:x1=1,x2=9;
答:每件商品应降价1元或9元;
②根据题意得出:
y=(100-80-x)(100+10x)
=-10x2+100x+2000,
当x=-$\frac{b}{2a}$=5时,y最大=2250元,
答:该经营者所获最大利润为2250元.
点评 此题主要考查了二次函数的应用以及一元二次方程的应用,注意单件利润×销售的商品的件数=总利润.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:解答题
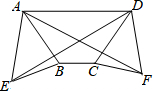 如图,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形DCF,连AF,DE.求证:AF=DE.
如图,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形DCF,连AF,DE.求证:AF=DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,在平面直角坐标系中,OA1=1,将OA1以O为旋转中心逆时针旋转90°到y轴OA2处,然后半径增加1个单位长度到A3,将OA3再以点O为旋转中心逆时针旋转90°到x轴OA4处,然后半径增加1个单位长度到A5,…,按图中规律进行下去,则点A2017的坐标为(1010,0).
如图所示,在平面直角坐标系中,OA1=1,将OA1以O为旋转中心逆时针旋转90°到y轴OA2处,然后半径增加1个单位长度到A3,将OA3再以点O为旋转中心逆时针旋转90°到x轴OA4处,然后半径增加1个单位长度到A5,…,按图中规律进行下去,则点A2017的坐标为(1010,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,AM⊥AD,交DC的延长线于点M,连接BM.
如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,AM⊥AD,交DC的延长线于点M,连接BM.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com