
【题目】在李村河治理工程实验过程中,某工程队接受一项开挖水渠的工程,所需天数y(天)与每天完成的工程量x(m/天)的函数关系图象如图所示,是双曲线的一部分. 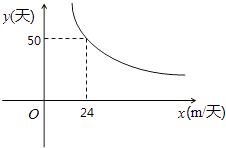
(1)请根据题意,求y与x之间的函数表达式;
(2)若该工程队有2台挖掘机,每台挖掘机每天能够开挖水渠15米,问该工程队需用多少天才能完成此项任务?
(3)如果为了防汛工作的紧急需要,必须在一个月内(按30天计算)完成任务,那么每天至少要完成多少米?
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=1,AD=![]() ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED。正确的是( )
,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED。正确的是( )
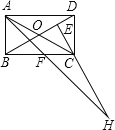
A. ②③ B. ②③④ C. ③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的面积为9,点
的面积为9,点![]() 在
在![]() 的边上运动.作点
的边上运动.作点![]() 关于原点
关于原点![]() 的对称点
的对称点![]() ,再以
,再以![]() 为边作等边
为边作等边![]() .当点
.当点![]() 在
在![]() 的边上运动一周时,点
的边上运动一周时,点![]() 随之运动所形成的图形面积为( )
随之运动所形成的图形面积为( )

A. 3 B. 9 C. 27 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD的边长为![]() 厘米,对角线AC上的两个动点E,F,点E从点A、点F从点C同时出发,沿对角线以1厘米/秒的相同速度运动,过E作EH⊥AC交Rt△ACD的直角边于H;过F作FG⊥AC交Rt△ACD的直角边于G,连接HG,EB.设HE,EF,FG,GH围成的图形面积为
厘米,对角线AC上的两个动点E,F,点E从点A、点F从点C同时出发,沿对角线以1厘米/秒的相同速度运动,过E作EH⊥AC交Rt△ACD的直角边于H;过F作FG⊥AC交Rt△ACD的直角边于G,连接HG,EB.设HE,EF,FG,GH围成的图形面积为![]() ,AE,EB,BA围成的图形面积为
,AE,EB,BA围成的图形面积为![]() (这里规定:线段的面积为
(这里规定:线段的面积为![]() ).E到达C,F到达A停止.若E的运动时间为x秒,解答下列问题:
).E到达C,F到达A停止.若E的运动时间为x秒,解答下列问题:
(1)如图①,判断四边形EFGH是什么四边形,并证明;
(2)当0<x<8时,求x为何值时,![]() ;
;
(3)若![]() 是
是![]() 的和,试用x的代数式表示y.(图②为备用图)
的和,试用x的代数式表示y.(图②为备用图)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的情况(记向东为正)记录如下(x>5且x<14,单位:m):
行驶次数 | 第一次 | 第二次 | 第三次 | 第四次 |
行驶情况 | x | ﹣ | x﹣3 | 2(5﹣x) |
行驶方向(填“东”或“西”) |
|
|
|
|
(1)请将表格补充完整;
(2)求经过连续4次行驶后,这辆出租车所在的位置;
(3)若出租车行驶的总路程为41m,求第一次行驶的路程x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A、B表示的数分别是-4、8(A、B两点间的距离用AB表示),点M、N是数轴上两个动点,分别表示数m、n
(1) AB=______个单位长度;若点M在A、B之间,则|m+4|+|m-8|=___________
(2) 若|m+4|+|m-8|=20,求m的值
(3) 若点M、点N既满足|m+4|+n=6,也满足|n-8|+m=28,则m=________;n=________
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了更好的开展“学校特色体育教育”,从全校八年级各班随机抽取了60学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图: 某校60名学生体育测试成绩成绩统计表
成绩 | 划记 | 频数 | 频率 |
优秀 | 正正正 | a | 0.3 |
良好 | 正正正正正正 | 30 | b |
合格 | 正 | 9 | 0.15 |
不合格 |
| c | d |
合计 |
(说明:40﹣55分为不合格,55﹣70分为合格,70﹣85分为良好,85﹣100分为优秀)
请根据以上信息,解答下列问题:
(1)表中的a=;b=;c=;d= .
(2)请根据频数分布表,画出相应的频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0, ![]() ),点A坐标为(﹣1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(﹣1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数关系表达式.
(2)点F为线段AC上一动点,过F作FE⊥x轴,FG⊥y轴,垂足分别为E、G,当四边形OEFG为正方形时,求出F点的坐标.
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com