
 把矩形ABCD沿着CE折叠,使得点B落在DB上,若AB=8,BC=10,则折痕线CE=5$\sqrt{5}$.
把矩形ABCD沿着CE折叠,使得点B落在DB上,若AB=8,BC=10,则折痕线CE=5$\sqrt{5}$. 分析 先在Rt△DCF中,求出DF,再在Rt△AEF中,利用勾股定理即可解决问题.
解答 解: ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠D=90°,
∵△CEF是由△CEB翻折得到,
∴BC=CF=10,∵AB=CD=8,
∴DF=$\sqrt{C{F}^{2}-C{D}^{2}}$=6,
∴AF=AD-DF=4,
设BE=EF=x,
在Rt△AEF中,∵AE2+AF2=EF2,
∴(8-x)2+42=x2,
∴x=5,
∴在Rt△BEC中,CE=$\sqrt{B{E}^{2}+B{C}^{2}}$=$\sqrt{{5}^{2}+1{0}^{2}}$=5$\sqrt{5}$,
故答案为$5\sqrt{5}$.
点评 本题考查矩形的性质、翻折变换、勾股定理等知识,灵活运用勾股定理是解题的关键,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
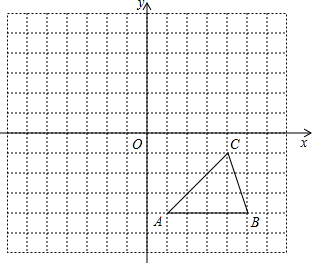 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1)
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△AED对折至△AFE,延长EF交边BC于点G,连接AG,CF,下列结论:①△ABG≌△AFG;②FG=FC;③AG∥CF;④S△FGC=$\frac{18}{5}$,其中正确结论是①③④(填序号).
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△AED对折至△AFE,延长EF交边BC于点G,连接AG,CF,下列结论:①△ABG≌△AFG;②FG=FC;③AG∥CF;④S△FGC=$\frac{18}{5}$,其中正确结论是①③④(填序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,墙A处需要维修,A处距离墙脚C处8米,墙下是一条宽BC为6米的小河,现要架一架梯子维修A处的墙体,现有一架12米长的梯子,问这架梯子能否到达墙的A处?
如图,墙A处需要维修,A处距离墙脚C处8米,墙下是一条宽BC为6米的小河,现要架一架梯子维修A处的墙体,现有一架12米长的梯子,问这架梯子能否到达墙的A处?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com