
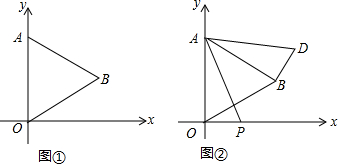
分析 (1)过B作BC⊥y轴于C,根据等边三角形的性质得到AC=OC=$\frac{1}{2}$AO=2,∠AOB=60°,解直角三角形即可得到结论;
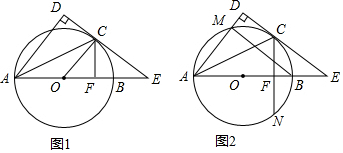
(2)由△ABD由△AOP旋转得到,利用旋转的性质得到两三角形全等,利用全等三角形对应边相等,对应角相等得到AP=AD,∠DAB=∠PAO,进而得到三角形ADP为等腰直角三角形,求出AP的长,即为等边三角形的边长,如图1,过点D作DH⊥x轴于点H,延长EB交DH于点G,可得BG⊥DH,在直角三角形BDG中,求出BG与DG的长,进而确定出OH与DH的长,确定出D坐标即可.
解答 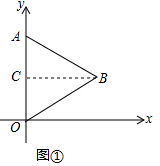 解:(1)过B作BC⊥y轴于C,
解:(1)过B作BC⊥y轴于C,
∵点A(0,4),
∴OA=4,
∵△AOB是等边三角形,
∴AC=OC=$\frac{1}{2}$AO=2,∠AOB=60°,
∴BC=$\sqrt{3}$OC=2$\sqrt{3}$,
∴B(2$\sqrt{3}$,2);
(2)∵△ABD由△AOP旋转得到,
∴△ABD≌△AOP,
∴AP=AD,∠DAB=∠PAO,
∴∠DAP=∠BAO=60°,
∴△ADP是等边三角形,
∴DP=AP=$\sqrt{{4}^{2}+(\sqrt{3})^{2}}$=$\sqrt{19}$,
如图1,过点D作DH⊥x轴于点H,延长EB交DH于点G,可得BG⊥DH,
在Rt△BDG中,∠BGD=90°,∠DBG=60°,BD=OP=$\sqrt{(\sqrt{19})^{2}-{4}^{2}}$=$\sqrt{3}$,
∴BG=BD•cos60°=$\sqrt{3}$×$\frac{1}{2}$=$\frac{\sqrt{3}}{2}$,DG=BD•sin60°=$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=$\frac{3}{2}$,
∴OH=EG=$\frac{5\sqrt{3}}{2}$,DH=$\frac{7}{2}$,
∴点D的坐标为($\frac{5\sqrt{3}}{2}$,$\frac{7}{2}$).
点评 本题考查了待定系数法确定一次函数解析式,坐标与图形性质,等边三角形的判定与性质,旋转的性质,锐角三角函数定义,以及勾股定理,熟练掌握性质及定理是解本题的关键.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
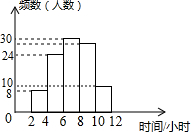 为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘制成如图所示的频数直方图,已知该校共有1000名学生,据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )
为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘制成如图所示的频数直方图,已知该校共有1000名学生,据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )| A. | 280 | B. | 240 | C. | 300 | D. | 260 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com