
【题目】如图,△ABC的外角∠ACD的平分线CP与∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP的度数是( )
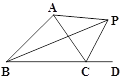
A. 30°; B. 40°; C. 50°; D. 60°.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校八年级学生在学习《数据的分析》后,进行了检测,现将该校八(1)班学生的成绩统计如下表,并绘制成条形统计图(不完整). 
分数(分) | 人数(人) |
68 | 4 |
78 | 7 |
80 | 3 |
88 | 5 |
90 | 10 |
96 | 6 |
100 | 5 |
(1)补全条形统计图;
(2)该班学生成绩的平均数为86.85分,写出该班学生成绩的中位数和众数;
(3)该校八年级共有学生500名,估计有多少学生的成绩在96分以上(含96分)?
(4)小明的成绩为88分,他的成绩如何,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=10,AC=2![]() ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.
【答案】10或6
【解析】试题解析:根据题意画出图形,如图所示,

如图1所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD-CD=8-2=6,
则BC的长为6或10.
【题型】填空题
【结束】
12
【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣4,0)两点,
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)设此抛物线与直线y=﹣x在第二象限交于点D,平行于y轴的直线 ![]() 与抛物线交于点M,与直线y=﹣x交于点N,连接BM、CM、NC、NB,是否存在m的值,使四边形BNCM的面积S最大?若存在,请求出m的值,若不存在,请说明理由.
与抛物线交于点M,与直线y=﹣x交于点N,连接BM、CM、NC、NB,是否存在m的值,使四边形BNCM的面积S最大?若存在,请求出m的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,M,N分别在BC,AC上,且BM=CN现有以下四个结论:
①DN=DM; ② ∠NDM=90°; ③ 四边形CMDN的面积为4; ④△CMN的面积最大为2.
其中正确的结论有( )

A. ①②④; B. ①②③; C. ②③④; D. ①②③④.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是以BC为直径的△ABC的外接圆,OP∥AC,且与BC的垂线交于点P,OP交AB于点D,BC、PA的延长线交于点E. 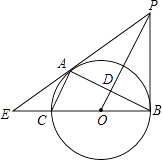
(1)求证:PA是⊙O的切线;
(2)若sinE= ![]() ,PA=6,求AC的长.
,PA=6,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.
![]() 若
若![]() ,则
,则![]() 的度数为______;
的度数为______;
![]() 若
若![]() ,求
,求![]() 的度数;
的度数;
![]() 猜想
猜想![]() 与
与![]() 之间存在什么数量关系?并说明理由;
之间存在什么数量关系?并说明理由;
![]() 当
当![]() 且点E在直线AC的上方时,这两块三角尺是否存在AD与BC平行的情况?若存在,请直接写出
且点E在直线AC的上方时,这两块三角尺是否存在AD与BC平行的情况?若存在,请直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com