
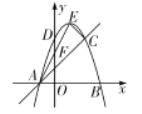
【题目】如图,在平面直角坐标系xOy中,抛物线![]() 与x轴交于A,B两点,与y轴交于点D,过点A的直线交抛物线于另一点C,点E为抛物线的顶点,连接CE,AE,设AE交y轴于点F,点A的坐标为
与x轴交于A,B两点,与y轴交于点D,过点A的直线交抛物线于另一点C,点E为抛物线的顶点,连接CE,AE,设AE交y轴于点F,点A的坐标为![]() ,且
,且![]() ,C、D两点关于对称轴对称.
,C、D两点关于对称轴对称.

(1)若![]() ,求抛物线的解析式;
,求抛物线的解析式;
(2)在(1)的条件下,试探究抛物线上是否存在一点M,使![]() 为以AC为直角边的直角三角形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由;
为以AC为直角边的直角三角形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由;
(3)设点P是直线AE上方抛物线上的一动点,若![]() 的面积最大值为
的面积最大值为![]() ,求a的值.
,求a的值.
【答案】(1)![]() ;(2)存在,点M的坐标为
;(2)存在,点M的坐标为![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)过点E作![]() 轴于点G,根据三角形中位线的性质求得点E的坐标,利用顶点式即可求得抛物线的解析式;
轴于点G,根据三角形中位线的性质求得点E的坐标,利用顶点式即可求得抛物线的解析式;
(2)作解图的辅助线,根据等腰直角三角形的判定和性质求得点![]() 的坐标,求得直线AC的解析式及与直线AC相互垂直的直线
的坐标,求得直线AC的解析式及与直线AC相互垂直的直线![]() 的解析式,联立直线
的解析式,联立直线![]() 与抛物线的解析式即可求得点
与抛物线的解析式即可求得点![]() 的坐标;
的坐标;
(3)先求得点A、B的坐标,设抛物线的表达式为![]() ,分别求得点E、F的坐标,设
,分别求得点E、F的坐标,设![]() ,求得经过A、P两点的直线解析式,利用三角形的面积公式及二次的最值即可求得答案.
,求得经过A、P两点的直线解析式,利用三角形的面积公式及二次的最值即可求得答案.
(1)如图,过点E作![]() 轴于点G,
轴于点G,
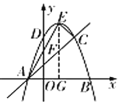
∵![]() ,
,
∴F为AE的中点,
又∵![]() ,
,
∴O为AC的中点,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴点E的坐标为![]() ,
,
∵点E为抛物线的顶点,
∴设抛物线的解析式为![]() ,
,
将点![]() 代入得
代入得![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为![]() ;
;
(2)存在.
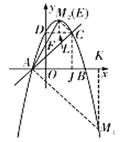
如图,分别过点A、C作![]() ,
,![]() 分别交抛物线于点
分别交抛物线于点![]() 、
、![]() ,过点
,过点![]() 作
作![]() 轴于点K,过点C作
轴于点K,过点C作![]() 轴于点J,连接CD、
轴于点J,连接CD、![]() ,过点
,过点![]() 作
作![]() 于点L.
于点L.
由(1)得![]() ,
,
∴![]() ,
,
∵顶点![]() ,
,
∴抛物线的对称轴为直线![]() ,
,
∵C、D两点关对称轴对称,
∴![]() ,
,
①![]() 时,
时,
∵![]() ,
,
∴∠CAJ=∠ACJ=45![]() ,
,
∴∠![]() AK=90
AK=90![]() ∠CAJ=45
∠CAJ=45![]() ,
,
∴![]() ,
,
设![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,化简得
,化简得![]() ,
,
解得 :![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
②当![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设直线AC的解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,
,
将![]() ,
,![]() ,代入
,代入![]() 得:
得:
![]() ,解得
,解得![]()
∴直线AC的解析式为![]() ,
,
∵![]() ,
,
∴![]() ,即直线
,即直线![]() 的解析式
的解析式![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
联立直线![]() 与抛物线的解析式得
与抛物线的解析式得![]() ,
,
解得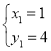 或
或 (与点C重合),
(与点C重合),
∴![]() ,即点
,即点![]() 与点E重合,
与点E重合,
综上所述,点M的坐标为![]() 或
或![]() ;
;
(3)由(1)得![]() ,抛物线的对称轴为直线
,抛物线的对称轴为直线![]() ,
,
∵![]() ,
,
∴![]()
设抛物线的表达式为![]() ,
,
即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点P是直线AE上方抛物线上的动点,
如图,设![]() ,连接AP,直线AP与y轴交于点Q,
,连接AP,直线AP与y轴交于点Q,
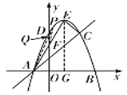
设经过A、P两点的直线解析式为![]() ,
,
则![]() ,解得
,解得![]() ,
,
∴经过A、P两点的直线解析式为![]() ,
,
∴点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 的面积最大值为
的面积最大值为![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,顶点为
,顶点为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]()

(1)求抛物线的顶点坐标(用含![]() 的式子表示);
的式子表示);
(2)![]() 的长是否与
的长是否与![]() 值有关,说明你的理由;
值有关,说明你的理由;
(3)设![]() ,求
,求![]() 的取值范围;
的取值范围;
(4)以![]() 为斜边,在直线
为斜边,在直线![]() 的左下方作等腰直角三角形
的左下方作等腰直角三角形![]() .设
.设![]() ,直接写出
,直接写出![]() 关于
关于![]() 的函数解析式及自变量
的函数解析式及自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一农户要建一个矩形猪舍,猪舍的一边利用长为15m的住房墙,另外三边用27m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长,宽分别为多少米时,猪舍面积为96m2?

查看答案和解析>>
科目:初中数学 来源: 题型:
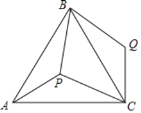
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4, PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.
查看答案和解析>>
科目:初中数学 来源: 题型:
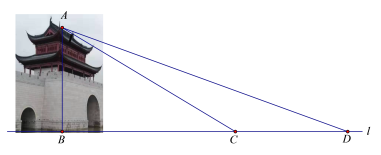
【题目】水城门位于淀浦河和漕港河三叉口,是环城水系公园淀浦河梦蝶岛区域重要的标志性景观.在课外实践活动中,某校九年级数学兴趣小组决定测量该水城门的高.他们的操作方法如下:如图,先在D处测得点A的仰角为20°,再往水城门的方向前进13米至C处,测得点A的仰角为31°(点D、C、B在一直线上),求该水城门AB的高.(精确到0.1米)
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
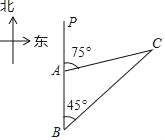
【题目】如图,一艘轮船以每小时40海里的速度在海面上航行,当该轮船行驶到B处时,发现灯塔C在它的东北方向,轮船继续向北航行,30分钟后到达A处,此时发现灯塔C在它的北偏东75°方向上,求此时轮船与灯塔C的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“五四青年节”来临之际,某校举办了以“我的青春我做主”为主题的演讲比赛. 并从参加比赛的学生中随机抽取部分学生的演讲成绩进行统计(等级:A:优秀,B:良好,C:一般,D:较差),并制作了如下统计图表(部分信息未给出):
等级 | 人数 |
A | m |
B | 20 |
C | n |
D | 10 |

请根据统计图表中的信息解答下列问题:
(1)这次共抽取了________名参加演讲比赛的学生,统计图中a=________,b=________;
(2)若该校学生共有2000人,如果都参加了演讲比赛,请你估计成绩达到优秀的有多少人?
(3)若演讲比赛成绩为A等级的学生中恰好有2名女生,其余的学生为男生,从A等级的学生中抽取两名同学参加全市演讲比赛,求抽中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
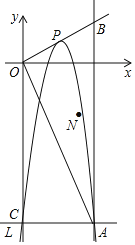
【题目】如图,点P为抛物线L:y=a(x﹣2)(x﹣4)(其中a为常数,且a<0)的顶点,L与y轴交于点C,过点C作x轴的平行线,与L交于点A,过点A作x轴的垂线,与射线OP交于点B,连接OA
(1)a=﹣2时,点P的坐标是 ,点B的坐标是 ;
(2)是否存在a的值,使OA=OB?若存在,求出a的值;若不存在,请说明理由
(3)若△OAB的外心N的坐标为(p,q),则
①当点N在△OAB内部时,求a的取值范围;
②用a表示外心N的横坐标p和纵坐标q,并求p与q的关系式(不写q的取值范围).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com