
����Ŀ��D��E�ֱ��Dz��ȱ�������ABC����AB��BC��AC���ı�AB��AC���е㣬O����ABC����ƽ���ϵĶ��㣬����OB��OC����G��F�ֱ���OB��OC���е㣬˳�����ӵ�D��G��F��E��
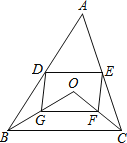
��1����ͼ������O����ABC���ڲ�ʱ����֤���ı���DGFE��ƽ���ı��Σ�
��2�����ı���DGFE�����Σ���OA��BCӦ����������������ϵ��Ϊʲô��
��3����OA��BC���� ʱ���ı���DGEF��һ�����Σ�ֱ����𰸣�����֤������
���𰸡���1������������2��AO=BC����3��OA��BC��
��������
�����������1������������������λ�ߵ����ʵó�DE��BC��DE=![]() BC��ͬ����GF��BC��GF=
BC��ͬ����GF��BC��GF=![]() BC�����ɵó�DE��GF��DE=GF���ɵó��ı���DGFE��ƽ���ı��Σ�
BC�����ɵó�DE��GF��DE=GF���ɵó��ı���DGFE��ƽ���ı��Σ�
��2�����ã�1��������ֻҪ�ڱ�����ȼ��ɵó��𰸣�
��3�����ã�1��������ֻҪ�ڱ����ֱ��ƽ���ı��μ�Ϊ���Σ�
��1��֤������D��E�ֱ��DZ�AB��AC���е㣮
��DE��BC��DE=![]() BC��
BC��
ͬ����GF��BC��GF=![]() BC��
BC��
��DE��GF��DE=GF��
���ı���DEFG��ƽ���ı��Σ�
��2���⣺�ⷨһ����O��λ����������Ҫ��AO=BC���ҵ�O��������CD������BE�ϣ�
���ɣ�1���ó��ı���DEFG��ƽ���ı��Σ�
����O��λ����������Ҫ��AO=BC���ҵ�O��������CD������BE��ʱ��
�ɵ�GD=![]() AO��GF=
AO��GF=![]() BC��
BC��
��DG=GE��
��ƽ���ı���DEFG�����Σ�
�ⷨ������O����AΪԲ�ģ�BCΪ�뾶��һ��Բ�ϣ�������������CD������BE����A�Ľ��㣮
�ⷨ��������A��BC��ƽ����l����O����AΪԲ�ģ�BCΪ�뾶��һ��Բ�ϣ���������l����A���������㣮
��3���ɣ�1��֪���ı���DEFG��ƽ���ı��Σ�
��OA��BCʱ��DG��GF��
��ƽ���ı���DGFE�Ǿ��Σ�
�ʴ��ǣ�OA��BC��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���E��F�ֱ���BC��CD�ϣ���AEF�ǵȱ������Σ�����AC��EF��G�����н��ۣ���BE=DF���ڡ�DAF=15�㣬��AC��ֱƽ��EF����BE+DF=EF����S��CEF=2S��ABE.������ȷ�����У���������
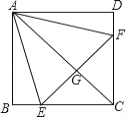
A. 4 B. 3 C. 2 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ε��ڲ�����һ���㵽��������������ľ�����ȣ��������һ���������Σ�������
A. �������ߵĽ���
B. ������ƽ���ߵĽ���
C. �����ߵĴ�ֱƽ���ߵĽ���
D. �����ߵĽ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵʩ���ʽ���������ij��ѧ������ѧ����������չ�����������γ���Դ�������꼶������������ѧϰС�飬���������꼶ѧ���μ�����ѧϰС���ͳ�Ʊ�������ͳ��ͼ���������ͼ�����ṩ����Ϣ�ش��������⣮
ѧϰС�� | ���� | ���� | �Ƽ� | ���� | д�� | ���� |
���� | 72 | 36 | 54 | 18 |
��1�����꼶����ѧ�� �ˣ�
��2���ڱ����еĿո�������Ӧ�����֣�
��3�����������ṩ���������ݵ���λ���� ��
��4�������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ȷ���ǣ� ��
A.��һ���ڱ���ȵ��ı���������
B.��һ������ֱ�ǵ�ƽ���ı����Ǿ���
C.�Խ��ߴ�ֱ��ƽ���ı�����������
D.һ��Ա�ƽ�е��ı�����ƽ���ı���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������2������+2������ô����3�������� ��
A. -3�� B. -2�� C. +3�� D. +2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ� ��
A. m2+m=3m3 B. ��m2��3 =m5 C. (2m)2 =2m2 D. m ��m2=m3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������κ���y=��a+1��x2+3x+a2��1��ͼ��ԭ�㣬��a��ֵ��Ϊ�� ��.
A.1��1
B.��1
C.0
D.1
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com