
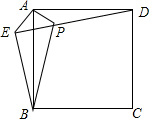
 ��֪����ͼ����������ABCD��ȡһ��E������AE��BE��DE������A��AE�Ĵ��߽�ED�ڵ�P����AE=AP=1��PB=$\sqrt{5}$�����н��ۣ�
��֪����ͼ����������ABCD��ȡһ��E������AE��BE��DE������A��AE�Ĵ��߽�ED�ڵ�P����AE=AP=1��PB=$\sqrt{5}$�����н��ۣ�| A�� | �٢ۢ� | B�� | �٢ڢ� | C�� | �ۢܢ� | D�� | �٢ۢ� |
���� ���ڡ�EAP=90�㣬���ԡ�EAB=��DAP������ΪAP=AE��AD=AB�����ԡ�APD�ա�DAP���Ӷ��ó���EBA=��PDA������֪��BED=��BAD=90�㣬����B��BF��AE����AE���ӳ����ڵ�F�����ԡ�BFE�ǵ���ֱ�������Σ��ɹ��ɶ��������BE��BF�ij��ȣ��Ӷ������AB2����������ABCD�����������S��APD+S��APB=S��AEB+S��APB=S��AEP+S��PEB�����������AEP���PEB��������ɣ�
��� �⣺��������ABCD�У�
AB=AD����BAD=90�㣬
�ߡ�EAP=90�㣬
���EAB+��BAP=��DAP+��BAP��
���EAB=��DAP��
�ڡ�APD���AEB�У�
$\left\{\begin{array}{l}{AP=AE}\\{��EAB=��DAP}\\{AD=AB}\end{array}\right.$��
���APD�ա�AEB��SAS����
�ʢ���ȷ��
�ߡ�APD�ա�AEB��
���EBA=��PDA��
���BED=��BAD=90�㣬
��BE��ED��
�ʢ���ȷ��
����B��BF��AE����AE���ӳ����ڵ�F��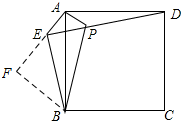
�ߡ�EAP=90�㣬
AE=AP��
���AEP=45�㣬
�ߡ�FEB+��AEP=90�㣬
��FEB+��EBF=90�㣬
���AEP=��EBF=45�㣬
��EF=BF��
��AE=AP=1��
���ɹ��ɶ�������ã�EP=$\sqrt{2}$��
��PB=$\sqrt{5}$��
���ɹ��ɶ�������ã�BE=$\sqrt{3}$��
��EF2+BF2=2BF2=BE2��
��BF=$\frac{\sqrt{6}}{2}$��
�ʢڴ���
��BF=EF=$\frac{\sqrt{6}}{2}$��
��AF=AE+EF=1+$\frac{\sqrt{6}}{2}$��
���ɹ��ɶ�����֪��AB2=AF2+BF2=4+$\sqrt{6}$��
�ʢ���ȷ��
�ߡ�APD�ա�AEB��
��S��APD=S��AEB��
��S��APD+S��APB
=S��AEB+S��APB
=S��AEP+S��PEB
=$\frac{1}{2}$+$\frac{\sqrt{6}}{2}$��
�ʢݴ���
��ѡ��A��
���� ���⿼���ı��ε��ۺ����⣬�漰ȫ�������ε��������ж������ɶ����������������ʽ��֪ʶ���ݣ��ۺϳ̶ȸߣ���Ҫѧ���������֪ʶ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǡ�O��ֱ����C��DΪ��O�����㣬CF��AB�ڵ�F��CE��AD��AD���ӳ����ڵ�E���� CE=CF������CA��CD��CB��
��ͼ��AB�ǡ�O��ֱ����C��DΪ��O�����㣬CF��AB�ڵ�F��CE��AD��AD���ӳ����ڵ�E���� CE=CF������CA��CD��CB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
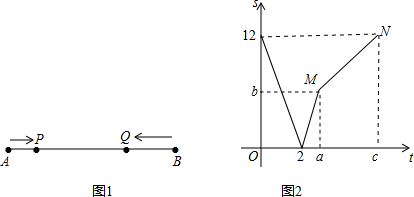
 ��ƽ��ֱ������ϵ�У����ɸ��뾶Ϊ2����λ���ȣ�Բ�Ľ�Ϊ60����������һ�����������ߣ���P��ԭ��O����������������������������˶�������ֱ���ϵ��ٶ�Ϊÿ��2����λ���ȣ����ڻ����ϵ��ٶ�Ϊÿ��$\frac{2��}{3}$����λ���ȣ���2015��ʱ����P�������ǣ�������
��ƽ��ֱ������ϵ�У����ɸ��뾶Ϊ2����λ���ȣ�Բ�Ľ�Ϊ60����������һ�����������ߣ���P��ԭ��O����������������������������˶�������ֱ���ϵ��ٶ�Ϊÿ��2����λ���ȣ����ڻ����ϵ��ٶ�Ϊÿ��$\frac{2��}{3}$����λ���ȣ���2015��ʱ����P�������ǣ�������| A�� | ��2015��0�� | B�� | ��2015��$\sqrt{3}$�� | C�� | ��2015��-$\sqrt{3}$�� | D�� | ��2016��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y1��y2��y3 | B�� | y2��y3��y1 | C�� | y2��y1��y3 | D�� | y1��y3��y2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
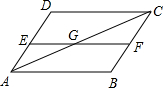 ��ͼ��AB��CD��EF��BC��AD��ACƽ�֡�BAD����ͼ�����AGE��ȵĽǣ�������
��ͼ��AB��CD��EF��BC��AD��ACƽ�֡�BAD����ͼ�����AGE��ȵĽǣ�������| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com