
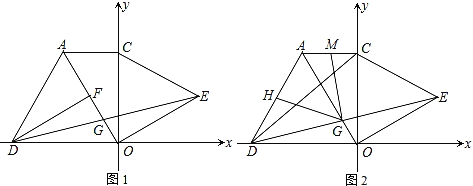
【题目】如图,在平面直角坐标系中,∠ACO=90°,∠AOC=30°,分别以AO、CO为边向外作等边三角形△AOD和等边三角形△COE,DF⊥AO于F,连DE交AO于G.
(1)求证:△DFG≌△EOG;
(2)H为AD的中点,连HG,求证:CD=2HG;
(3)在(2)的条件下,AC=4,若M为AC的中点,求MG的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)本题考查全等三角形的判定,通过等边三角形的性质利用AAS定理解答本题.
(2)本题考查三角形中位线定理以及全等三角形的判定,通过构造辅助线利用SAS定理解答.
(3)本题考查三角形中位线定理以及等边三角形的证明,通过构造辅助线,结合角度的计算加以证明,最后求解边长.
证明:(1)如图1,∵∠AOC=30°,
∴∠GOE=90°.
设AC=a,则OA=2a,OE=OC=![]() a,
a,
在等边△AOD中,DF⊥OA,
∴DF=![]() a,
a,
∴DF=OE.
又∵∠DGF=∠EGO,∠DFG=∠EOG,
∴△DFG≌△EOG(AAS).
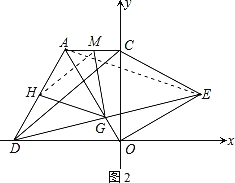
(2)如下图图2所示,连接AE,
∵H、G分别为AD、DE的中点,
∴HG∥AE,HG=![]() AE.
AE.
∵DO=AO,CO=OE,∠DOC=∠AOE=90°,
∴△DOC≌△AOE(SAS),
∴DC=AE,
∴DC=2HG.
(3)如下图图2所示,连接HM,
∵H、M分别为AD、AC的中点,
∴HM=![]() CD.
CD.
∵DC=2HG,
∴HM=HG.
又∠DHG=∠DAE=60°+∠OAE=60°+∠ODC,∠AHM=∠ADC,
∴∠MHG=180°﹣∠AHM﹣∠DHG=180°﹣∠ADC﹣60°﹣∠ODC=120°﹣(∠ADC+∠ODC)=120°﹣∠ADO=60°,
∴△HMG为等边三角形.
∵AC=4,
∴OA=OD=8,OC=![]() ,CD=
,CD=![]() ,
,
∴MG=HG=![]() CD=
CD=![]() .
.


科目:初中数学 来源: 题型:
【题目】下列各数填在相应的集合内,注意数与数要用逗号隔开
![]() ,
,![]() ,0 ,
,0 ,![]() ,8 ,-2 ,25% ,-3.8 ,0.1011 ,100 ,-200
,8 ,-2 ,25% ,-3.8 ,0.1011 ,100 ,-200
负数集合:{ …};
整数集合:{ … };
非负集合:{ … };
分数集合:{ … };
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向右移动了3个单位长度,再向左移动 5 个单位长度,可以看到终点表示的数是![]() .已知点
.已知点![]() 、
、![]() 是数轴上的点,完成下列各题:
是数轴上的点,完成下列各题:
![]()
(1)如果点![]() 表示数- 3,将点
表示数- 3,将点![]() 向右移动 7 个单位长度,那么终点
向右移动 7 个单位长度,那么终点![]() 表示的数是 ,
表示的数是 ,![]() 、
、![]() 两点间的距离是 .
两点间的距离是 .
(2)如果点![]() 表示数是3,将点
表示数是3,将点![]() 向左移动 7 个单位长度,再向右移动5 个单位长度,那么终点
向左移动 7 个单位长度,再向右移动5 个单位长度,那么终点![]() 表示的数是 ,
表示的数是 ,![]() 、
、 ![]() 两点间的距离是 .
两点间的距离是 .
(3)一般地,如果点![]() 表示数为
表示数为![]() ,将点
,将点![]() 向右移动
向右移动![]() 个单位长度,再向左移动
个单位长度,再向左移动![]() 个单位长度,那么请你猜想终点
个单位长度,那么请你猜想终点![]() 表示的数是 ,
表示的数是 ,![]() 、
、![]() 两点间的距离是 .
两点间的距离是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在4×4正方形的网格中,线段AB,CD如图位置,每个小正方形的边长都是1.
(1)求出线段AB、CD的长度;
(2)在图中画出线段EF,使得EF=![]() ,并判断以AB,CD,EF三条线段组成的三角形的形状,请说明理由;
,并判断以AB,CD,EF三条线段组成的三角形的形状,请说明理由;
(3)我们把(2)中三条线段按照点E与点C重合,点F与点B重合,点D与点A重合,这样可以得△ABC,则点C到直线AB的距离为______(直接写结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点![]() 表示的数是
表示的数是![]() 点
点![]() 在点
在点![]() 的右侧,且到点
的右侧,且到点![]() 的距离是18;点
的距离是18;点![]() 在点
在点![]() 与点
与点![]() 之间,且到点
之间,且到点![]() 的距离是到点
的距离是到点![]() 距离的2倍.
距离的2倍.
(1)点![]() 表示的数是____________;点
表示的数是____________;点![]() 表示的数是_________;
表示的数是_________;
(2)若点P从点![]() 出发,沿数轴以每秒4个单位长度的速度向右匀速运动;同时,点Q从点B出发,沿数轴以每秒2个单位长度的速度向左匀速运动。设运动时间为
出发,沿数轴以每秒4个单位长度的速度向右匀速运动;同时,点Q从点B出发,沿数轴以每秒2个单位长度的速度向左匀速运动。设运动时间为![]() 秒,在运动过程中,当
秒,在运动过程中,当![]() 为何值时,点P与点Q之间的距离为6?
为何值时,点P与点Q之间的距离为6?
(3)在(2)的条件下,若点P与点C之间的距离表示为PC,点Q与点B之间的距离表示为![]() 在运动过程中,是否存在某一时刻使得
在运动过程中,是否存在某一时刻使得![]() ?若存在,请求出此时点
?若存在,请求出此时点![]() 表示的数;若不存在,请说明理由.
表示的数;若不存在,请说明理由.
![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,正方形OABC的顶点B的坐标为(3,3),直线CD交直线OA于点D,直线OE交线段AB于E,且CD⊥OE,垂直为点F,若图中阴影部分的面积是正方形OABC的面积的![]() ,则△OFC的周长为________.
,则△OFC的周长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
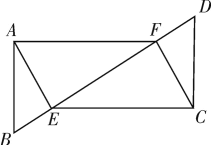
【题目】如图,AB∥CD,AB=CD,点E,F在BD上,∠BAE=∠DCF,连接AF,EC.
(1)求证:AE=FC;
(2)求证:四边形AECF是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com