
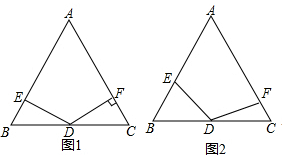
���� ��1�������ı��ε��ڽǺͼ��ɵõ����ۣ�
��2������ȫ�������ε��ж������ʼ��ɵõ����ۣ�
��3������AD������D��DM��AB��M����DN��AC��N����ͼ2���ɵ�D���߶�BC���е㣬�õ�AD�ǡ�BAC�Ľ�ƽ���ߣ����ݽ�ƽ���ߵ����ʵõ�DM=DN������ȫ�������ε����ʼ��ɵõ����ۣ�
��4����ͼ2��a���У�����D��DM��AB��M����DN��AC��N������ȫ�������ε����ʵõ�BM=CN��DM=DN��ME=NF�����ǵõ����ۣ�
��� �⣺��1����DF��AC��
���AFD=90�㣬
�ߡ�A=60�㣬��EDF=120?��
���AED=360��-��A-��AFD-��EDF=90�㣬
��DE��AB��
��2���ߡ�ABC�ǵȱ������Σ�
���B=��C=60�㣬
�ߵ�D���߶�BC���е㣬
��BD=CD��
�ڡ�BDE���CDF�У�$\left\{\begin{array}{l}{��BED=��CFD=90��}\\{��B=��C}\\{BD=CD}\end{array}\right.$��
���BED�ա�CFD��
��DE=DF��
��3����2���еĽ��ۻ���������AD��
����D��DM��AB��M����DN��AC��N����ͼ2��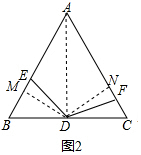
�ߵ�D���߶�BC���е㣬
��AD�ǡ�BAC�Ľ�ƽ���ߣ�
��DM=DN��
�ߡ�AMD=��BMD=��AND=��CND=90��
�ߡ�A=60�㣬
���MDN=360��-60��-90��-90��=120�㣮
�ߡ�EDF=120�㣬
���MDE=��NDF��
�ڡ�EMD�͡�FND�У�$\left\{\begin{array}{l}{��EMD=��FND}\\{DM=DN}\\{��MDE=��NDF}\\{\;}\end{array}\right.$��
���EMD�ա�FND��
��DE=DF��
��4����ͼ2��a���У�����D��DM��AB��M����DN��AC��N��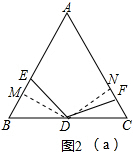 �ڡ�BDM���CDN�У�$\left\{\begin{array}{l}{��B=��C}\\{��BMD=��DNC=90��}\\{BD=CD}\end{array}\right.$��
�ڡ�BDM���CDN�У�$\left\{\begin{array}{l}{��B=��C}\\{��BMD=��DNC=90��}\\{BD=CD}\end{array}\right.$��
���BDM�ա�CDN��
��BM=CN��DM=DN��
�֡ߡ�EDF=120��=��MDN��
���EDM=��NDF��
�ڡ�DME���DNF�У�$\left\{\begin{array}{l}{��EDM=��FDN}\\{��DME=��DNF}\\{DM=DN}\end{array}\right.$��
���EDM�ա�FDN��
��ME=NF��
��BE+CF=BM+EM+NC-FN=2BM=BD=$\frac{1}{2}$AB��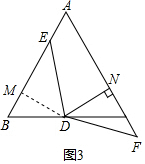
��ͼ3��ͬ��BM=CN��DM=DN��
�֡ߡ�EDF=120��=��MDN��
���EDM=��NDF��
�֡ߡ�EMD=��FND=90�㣬
���EDM�ա�FDN��
��ME=NF��
��BE-CF=BM+EM-��FN-CN��=2BM=BD=$\frac{1}{2}$AB��
�����������߶�BE��CF��AB֮���������ϵΪ��BE+CF=$\frac{1}{2}$AB��BE-CF=$\frac{1}{2}$AB��
���� ������Ҫ�����˵ȱ������ε��ж������ʡ��ı��ε��ڽǺͶ�����ȫ�������ε��ж������ʡ����Ǻ����Ķ��塢����ǵ����Ǻ���ֵ��֪ʶ��ͨ��֤��������ȫ�ȵõ�BM=CN��DM=DN��EM=FN�ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ABC���DEF����ֱ��MN��Գƣ������н����д�����ǣ�������
��ͼ����ABC���DEF����ֱ��MN��Գƣ������н����д�����ǣ�������| A�� | AB��DF | B�� | ��B=��E | ||
| C�� | AB=DE | D�� | AD�����߱�MN��ֱƽ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
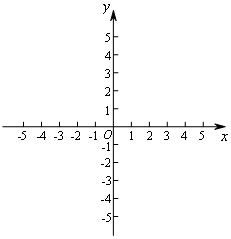 ��ƽ��ֱ������ϵxOy�У�ֱ��y=x-1��y�ύ�ڵ�A����˫����y=$\frac{k}{x}$���ڵ�B��m��2����
��ƽ��ֱ������ϵxOy�У�ֱ��y=x-1��y�ύ�ڵ�A����˫����y=$\frac{k}{x}$���ڵ�B��m��2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
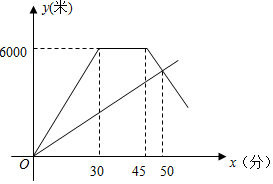 �����������6000�ף��������ΰͬʱ�Ӽس�������ǰ���ҵأ���������ҵغ���Ϣһ��ʱ�����ԭ�����ٶȴ�ԭ·���أ���ͼ��ʾ��������صľ���y���ף������ʱ��x���֣�֮��ĺ���ͼ��
�����������6000�ף��������ΰͬʱ�Ӽس�������ǰ���ҵأ���������ҵغ���Ϣһ��ʱ�����ԭ�����ٶȴ�ԭ·���أ���ͼ��ʾ��������صľ���y���ף������ʱ��x���֣�֮��ĺ���ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
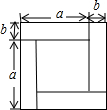 ��ͼ������ȫ��ͬ���ĸ�������ֽƬƴ��һ����������Σ������ֲ�ͬ�ķ�����ʾ����������ε����������Եó�һ����ʽΪ��������
��ͼ������ȫ��ͬ���ĸ�������ֽƬƴ��һ����������Σ������ֲ�ͬ�ķ�����ʾ����������ε����������Եó�һ����ʽΪ��������| A�� | ��a+b��2=a2+2ab+b2 | B�� | ��a-b��2=a2-2ab+b2 | C�� | a2-b2=��a+b����a-b�� | D�� | ��a+b��2=��a-b��2+4ab |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
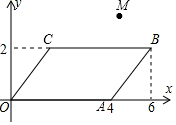 ��ͼ����ƽ��ֱ������ϵxOy�У��ı���OABC��ƽ���ı��Σ���A��4��0����B��6��2����M��4��3������ƽ������һ������M��ֱ�߽�ƽ���ı���OABC������ֳ���ȵ������֣���д����ֱ�ߵĺ�������ʽy=2x-5��
��ͼ����ƽ��ֱ������ϵxOy�У��ı���OABC��ƽ���ı��Σ���A��4��0����B��6��2����M��4��3������ƽ������һ������M��ֱ�߽�ƽ���ı���OABC������ֳ���ȵ������֣���д����ֱ�ߵĺ�������ʽy=2x-5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b | B�� | a=b | C�� | a��b | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com