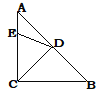
【题目】在等腰Rt△ABC中，D为斜边AB的中点，点E在AC上，且∠EDC=72°，点F在AB上，满足DE=DF，则∠CEF的度数为_______.
【答案】54°或144°
【解析】分析：分两种情况：①点F在AD上时，可求出∠DEF=81°，在△CDE中可求出∠CED=63°，故可求出∠CEF=144°；②点F在DB上时，可求出∠DEF=9°,故可求出∠CEF=54°.
详解：①点F在AD上时，如图1，
∵AC=BC,D是AB的中点，且∠ACB=90°,
∴∠ADC=90°，∠DCE=45°
∵∠CDE=72°
∴∠EDF=18°
∵DE=DF
∴∠DEF=81°
在△ECD中，∠CDE=72°,∠ECD=45°
∴∠CED=63°，
∴∠CEF=144°；
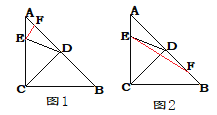
②点F在DB上时，如图2.
同理得，∠DEF=9°,
∴∠CEF=54°.
故答案为：54°或144°.
世纪百通期末金卷系列答案科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的边长是2，点E是CD边的中点，点F是边BC上不与点B，C重合的一个动点，把∠C沿直线EF折叠，使点C落在点C′处．当△ADC′为等腰三角形时，FC的长为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x的方程
=1的解为负数，且关于x、y的二元一次方程组
的解之和为正数，则下列各数都满足上述条件a的值的是（ ）
A. 
，2，5 B. 0，3，5 C. 3，4，5 D. 4，5，6
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函双y=
（m≠0）的阳象交于点c（n，3），与x轴、y轴分别交于点A、B，过点C作CM⊥x轴，垂足为M，若tan∠CAM=
，OA=2．
（1）求反比例函数和一次函数的解析式；
（2）点D是反比例函数图象在第三象限部分上的一点，且到x轴的距离是3，连接AD、BD，求△ABD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，Rt△ABC≌Rt△CED（∠ACB＝∠CDE＝90°），点D在BC上，AB与CE相交于点F
(1) 如图1，直接写出AB与CE的位置关系
(2) 如图2，连接AD交CE于点G，在BC的延长线上截取CH＝DB，射线HG交AB于K，求证：HK＝BK
查看答案和解析>>
科目：初中数学 来源： 题型：
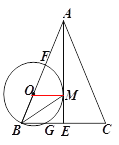
【题目】如图，在△ABC中,AB=AC,AE是BC边上的高线，BM平分∠ABC交AE于点M，经过B，M 两点的⊙O交BC于点G，交AB于点F ，FB为⊙O的直径．
（1）求证：AM是⊙O的切线
（2）当BE=3，cosC=
时，求⊙O的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】Rt△ABC中，∠ABC=90°，AB=3，BC=4，过点B的直线把△ABC分割成两个三角形，使其中只有一个是等腰三角形，则这个等腰三角形的面积是_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
