
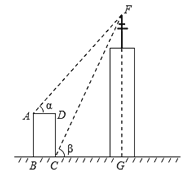
【题目】如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为∠α=48°和∠β=65°,矩形建筑物宽度AD=20m,高度CD=30m,则信号发射塔顶端到地面的高度FG为__米(结果精确到1m).
参考数据:sin48°=0.7,cos48°=0.7,tan48°=1.1,cos65°=0.4,tan65°=2.1
科目:初中数学 来源: 题型:
【题目】有这样一个题目:
按照给定的计算程序,确定使代数式n(n+2)大于2000的n的最小正整数值.想一想,怎样迅速找到这个n值,请与同学们交流你的体会.
小亮尝试计算了几组n和n(n+2)的对应值如下表:
n | 50 | 40 | |
n(n+2) | 2600 | 1680 |
(1)请你继续小亮的尝试,再算几组填在上表中(几组随意,自己画格),并写出满足题目要求的n的值;
(2)结合上述过程,对于“怎样迅速找到n值”这个问题,说说你的想法.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知顶点为P的抛物线C1的解析式为y=a(x-3)2(a≠0),且经过点(0,1).
(1)求a的值及抛物线C1的解析式;
(2)如图,将抛物线C1向下平移h(h>0)个单位得到抛物线C2,过点K(0,m2)(m>0)作直线l平行于x轴,与两抛物线从左到右分别相交于A,B,C,D四点,且A,C两点关于y轴对称.
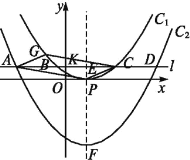
①点G在抛物线C1上,当m为何值时,四边形APCG为平行四边形?
②若抛物线C1的对称轴与直线l交于点E,与抛物线C2交于点F.试探究:在K点运动过程中,![]() 的值是否改变?若会,请说明理由;若不会,请求出这个值.
的值是否改变?若会,请说明理由;若不会,请求出这个值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:数学活动课上,乐老师给出如下定义:有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形.
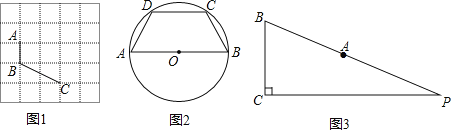
理解:(1)如图1,已知A、B、C在格点(小正方形的顶点)上,请在方格图中画出以格点为顶点,AB、BC为边的两个对等四边形ABCD;
(2)如图2,在圆内接四边形ABCD中,AB是⊙O的直径,AC=BD.求证:四边形ABCD是对等四边形;
(3)如图3,在Rt△PBC中,∠PCB=90°,BC=11,tan∠PBC=![]() ,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D,使四边形ABCD为对等四边形,并求出CD的长.
,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D,使四边形ABCD为对等四边形,并求出CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计.现从该校随机抽取![]() 名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
(1)求n的值;
(2)若该校学生共有1200人,试估计该校喜爱看电视的学生人数;
(3)若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名学生,求恰好抽到2名男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
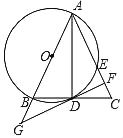
【题目】如图,△ABC中,AB=AC,以AB为直径的圆O交BC于D,交AC于点E,过点D作DF⊥AC于点F,交AB延长线于点G,连结AD.
(1)∠ADB= °,依据是 ;
(2)求证:DF是圆O的切线;
(3)已知BC=4![]() ,CF=2,求AE和BG的长.
,CF=2,求AE和BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大熊山某农家乐为了抓住“五一”小长假的商机,决定购进A、B两种纪念品。若购进A种纪念品4件,B种纪念品3件,需要550元;若购进A种纪念品8件,B种纪念品5件,需要1050元。
(1)求购进A、B两种纪念品每件各需多少元。
(2)若该农家乐决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该农家乐共有几种进货方案。
(3)若销售每件A种纪念品可获利润30元,每件B种纪念品可获利润20元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元。
查看答案和解析>>
科目:初中数学 来源: 题型:
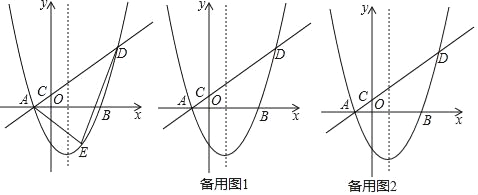
【题目】如图,在平面直角坐标系中,抛物线y=ax2﹣2ax﹣3a(a>0)与x轴交于A、B两点(点A在点B左侧),经过点A的直线l:y=kx+b与y轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)直接写出点A的坐标,并用含a的式子表示直线l的函数表达式(其中k、b用含a的式子表示).
(2)点E为直线l下方抛物线上一点,当△ADE的面积的最大值为![]() 时,求抛物线的函数表达式;
时,求抛物线的函数表达式;
(3)设点P是抛物线对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否为矩形?若能,求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分7分)
四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上.
(1)求随机抽取一张卡片,恰好得到数字2的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则见信息图.你认为这个游戏公平吗?请用列表法或画树状图法说明理由,若认为不公平,请你修改规则,使游戏变得公平.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com