
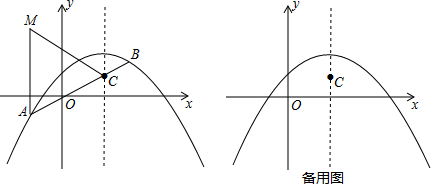
分析 (1)利用抛物线的对称性得到抛物线与x轴的另一个交点坐标为(-2,0),则可设交点式求抛物线解析式;
(2)利用抛物线的平移变换规律得到抛物线C2的解析式为y=-$\frac{1}{4}$(x-2)2+2,再确定直线y=kx-2k+1过定点(2,1),从而得到C(2,1),设A[x,-$\frac{1}{4}$(x-2)2+2)],然后利用两点的距离公式证明AC=AM;
(3)①直线y=3交直线x=2于D点,过点B作BE⊥直线y=3于点E,如图1,则利用(2)的结论可证明△ACM是等边三角形,BC=BE,易证∠MCD=60°,∠BCE=∠DCE=30°,利用解直角三角形得到$\frac{DE}{CD}$=$\frac{\sqrt{3}}{3}$,$\frac{CD}{DM}$=$\frac{\sqrt{3}}{3}$,所以$\frac{DE}{DM}$=$\frac{1}{3}$,然后根据平行线分线段成比例定理得到$\frac{CB}{CA}$=$\frac{DE}{DM}$=$\frac{1}{3}$;
②如图2,y轴与抛物线的交点记作点P,与直线y=3的交点记作点H,由(2)可知PC=PH,如图,在抛物线上取异于点P的P′,作P′H′⊥直线y=3于H′,P′Q⊥y轴于点Q,由(2)可知P′C=PH′,易得四边形HH′P′Q为矩形,则P′H′=QH,然后利用OP′>OQ得到OP+PH<OP′+P′C,于是可判断点P(0,1)使得PO+PC取得最小值.
解答 (1)解:∵抛物线C1的对称轴为直线x=2,且抛物线与x轴的一个交点坐标为(6,0),
∴抛物线与x轴的另一个交点坐标为(-2,0),
∴抛物线C1的解析式为y=-$\frac{1}{4}$(x+2)(x-6),
即y=-$\frac{1}{4}$x2+x+3;
(2)证明:∵抛物线C1的解析式为y=-$\frac{1}{4}$(x-2)2+4,
∴抛物线C2的解析式为y=-$\frac{1}{4}$(x-2)2+2,
∵直线y=kx-2k+1过定点(2,1),
而直线y=kx-2k+1交抛物线C2的对称轴于点C,
∴C(2,1),
设A[x,-$\frac{1}{4}$(x-2)2+2)],
∴AC2=(x-2)2+[-$\frac{1}{4}$(x-2)2+2-1]2=$\frac{1}{16}$(x-2)4+$\frac{1}{2}$(x-2)2+1,
AM2=[-$\frac{1}{4}$(x-2)2+2-3]2=$\frac{1}{16}$(x-2)4+$\frac{1}{2}$(x-2)2+1,
∴AC=AM;
(3)解:①∵AC=AM,CM=AM,
∴△ACM是等边三角形.
∴∠AMC=∠ACM=60°,
直线y=3交直线x=2于D点,过点B作BE⊥直线y=3于点E,如图1,则由(2)可知BC=BE,易证∠MCD=60°,∠BCE=∠DCE=30°,
在Rt△CDE中,tan∠DCE=tan30°=$\frac{DE}{CD}$=$\frac{\sqrt{3}}{3}$,
在Rt△CDM中,tan∠CMD=tan30°=$\frac{CD}{DM}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{DE}{DM}$=$\frac{1}{3}$,
∵AM∥DC∥EB,
∴$\frac{CB}{CA}$=$\frac{DE}{DM}$=$\frac{1}{3}$;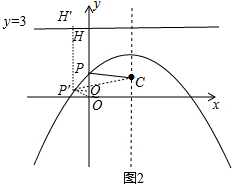 ②存在.
②存在.
如图2,y轴与抛物线的交点记作点P,与直线y=3的交点记作点H,
由(2)可知PC=PH,
如图,在抛物线上取异于点P的P′,作P′H′⊥直线y=3于H′,P′Q⊥y轴于点Q,
由(2)可知P′C=PH′,
易得四边形HH′P′Q为矩形,
∴P′H′=QH,
∵OP′>OQ,
∴OQ+QH<OP′+P′H′,
∴OP+PH<OP′+P′C,
∴点P(0,1)使得PO+PC取得最小值.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质、等边三角形的性质和平行线分线段成比例定理;会利用待定系数法求函数解析式;理解坐标与图形性质,记住两点间的距离公式;会解直角三角形.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的.其中测得坡长AB=600米,BC=200米,坡角∠BAF=30°,∠CBE=45°.(结果保留根号)
如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的.其中测得坡长AB=600米,BC=200米,坡角∠BAF=30°,∠CBE=45°.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
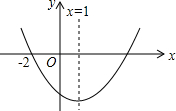 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b=0;②a+c>b;③抛物线y=ax2+bx+c与x轴的另一个交点为(3,0);④abc>0.其中正确的结论是①④(填写序号)
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b=0;②a+c>b;③抛物线y=ax2+bx+c与x轴的另一个交点为(3,0);④abc>0.其中正确的结论是①④(填写序号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
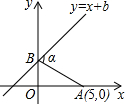 如图,已知点A的坐标为(5,0),直线y=x+b(b≥0)与y轴交于点B,连接AB,∠α=75°,则b的值为$\frac{5\sqrt{3}}{3}$.
如图,已知点A的坐标为(5,0),直线y=x+b(b≥0)与y轴交于点B,连接AB,∠α=75°,则b的值为$\frac{5\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,三架飞机P,Q,R保持编队飞行,某时刻在坐标系中的坐标分别为(-1,1),(-3,1),(-1,-1).30秒后,飞机P飞到P′(4,3)位置,则飞机Q,R的位置Q′,R′分别为( )
如图所示,三架飞机P,Q,R保持编队飞行,某时刻在坐标系中的坐标分别为(-1,1),(-3,1),(-1,-1).30秒后,飞机P飞到P′(4,3)位置,则飞机Q,R的位置Q′,R′分别为( )| A. | Q′(2,3),R′(4,1) | B. | Q′(2,3),R′(2,1) | C. | Q′(2,2),R′(4,1) | D. | Q′(3,3),R′(3,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 成绩 | 频率 |
| 60≤x<70 | 0.3 |
| 70≤x<80 | 0.4 |
| 80≤x<90 | 0.2 |
| 90≤x≤100 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 阅读数量 | 1本 | 2本 | 3本 | 3本以上 |
| 人数(人) | 10 | 18 | 13 | 4 |
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com