
【题目】用四舍五入法按要求取近似数:
(1)2367890(精确到十万位);(2)29524(精确到千位);
(3)4.2046(精确到千分位);(4)3.102(精确到百分位).
【答案】(1) 2400000(2) 30000 (3) 4.205(4) 3.10
【解析】
先找到每小题给出的精确位上的数字,再看它后一位数字是否大于等于5,是则舍掉后面所有数再向前进位,否则直接舍掉后面所有数字.
(1) 2367890万位数字是3,后一位数字是6,大于5,则舍掉后面所有数再向前进位,则2367890≈2400000=![]()
(2) 29524千位数字是9,后一位数字是5,等于5,则舍掉后面所有数向前进位,则29524≈30000=![]()
(3) 4.2046千分位数字是4,后一位是6,大于5,则舍掉后面所有数再向前进位,则4.2046≈4.205
(4) 3.102百分位数字是0,后一位是2,小于5,则直接舍掉后面所有数字,且0要保留,则3.102≈3.10
故答案为:(1)![]() (2)
(2)![]() (3) 4.205(4) 3.10
(3) 4.205(4) 3.10


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】已知有理数a、b、c在数轴上对应点如图所示,且|a|>|b|.
![]()
(1)|a﹣b|= ,|a+b|= ,|a+c|= ,|b﹣c|= ;
(2)化简|a﹣b|﹣|a+b|+|a+c|﹣|b﹣c|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a、b、c在数轴上的位置如图所示,且|a|=|b|,则下列结论中错误的是( )
![]()
A. a+c<0B. -a+b+c<0
C. |a+b|>|a+c|D. |a+b|<|a+c|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F,G分别在线段BC,AC上,抛物线P上的部分点的横坐标对应的纵坐标如下.

(1)求A,B,C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系式,并指出m的取值范围;
(3)当矩形DEFG的面积S最大时,连接DF并延长至点M,使FM=k·DF,若点M不在抛物线P上,求k的取值范围;
(4)若点D的坐标为(1,0),求矩形DEFG的面积.
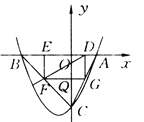
查看答案和解析>>
科目:初中数学 来源: 题型:
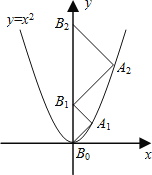
【题目】如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2015B2014B2015的腰长=____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元初,中美洲马雅人使用的一种数字系统与其他计数方式都不相同,它采用二十进位制但只有3个符号,用点“![]() ”、划“—”、卵形“
”、划“—”、卵形“![]() ”来表示我们所使用的自然数,如自然数1-19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
”来表示我们所使用的自然数,如自然数1-19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
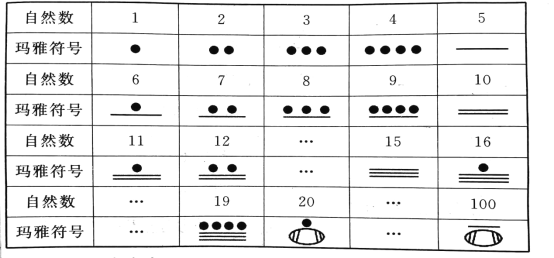
(1)玛雅符号![]() 表示的自然数是哪个数;
表示的自然数是哪个数;
(2)请你画出表示自然数280的玛雅符号.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,将点
中,将点![]() 翻折到对角线
翻折到对角线![]() 上的点
上的点![]() 处,折痕
处,折痕![]() 交
交![]() 于点
于点![]() .将点
.将点![]() 翻折到对角线
翻折到对角线![]() 上的点
上的点![]() 处,折痕
处,折痕![]() 交
交![]() 于点
于点![]() .
.
![]() 求证:四边形
求证:四边形![]() 为平行四边形;
为平行四边形;
![]() 若四边形
若四边形![]() 为菱形,且
为菱形,且![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+b x+c经过A,B,C三点,当x≥0时,其图象如图所示.
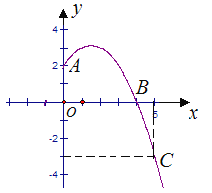
(1)求抛物线的解析式,写出抛物线的顶点坐标;
(2)画出抛物线y=ax2+b x+c当x<0时的图象;
(3)利用抛物线y=ax2+b x+c,写出x为何值时,y>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形,在图1正方形网格(每个小正方形边长为1)中画出格点△ABC,使AB=AC=5,BC=![]()
(2)在△ABC中, AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图2所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图2所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
①△ABC的面积为: .
②若△DEF三边的长分别为![]() 、
、![]() 、
、![]() ,请在图3的正方形网格中画出相应的△DEF,并利用构图法求出它的面积为_____________.
,请在图3的正方形网格中画出相应的△DEF,并利用构图法求出它的面积为_____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com