
【题目】如图,⊙O的半径r=25,四边形ABCD内接圆⊙O,AC⊥BD于点H,P为CA延长线上的一点,且∠PDA=∠ABD
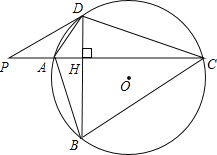
(1) 试判断PD与⊙O的位置关系,并说明理由
(2) 若tan∠ADB=![]() ,PA=
,PA=![]() AH,求BD的长
AH,求BD的长
【答案】(1)PD与圆O相切.理由见解析;(2)25![]()
【解析】
试题分析:(1)首先连接DO并延长交圆于点E,连接AE,由DE是直径,可得∠DAE的度数,又由∠PDA=∠ABD=∠E,可证得PD⊥DO,即可得PD与圆O相切于点D;
(2)首先由tan∠ADB=![]() ,可设AH=3k,则DH=4k,又由PA=
,可设AH=3k,则DH=4k,又由PA=![]() AH,易求得∠P=30°,∠PDH=60°,连接BE,则∠DBE=90°,DE=2r=50,可得BD=DE
AH,易求得∠P=30°,∠PDH=60°,连接BE,则∠DBE=90°,DE=2r=50,可得BD=DE![]() cos30°=25
cos30°=25![]()
试题解析:(1)PD与圆O相切.
理由:如图,连接DO并延长交圆于点E,连接AE,
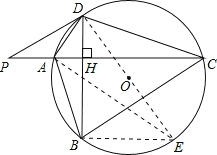
∵DE是直径,
∴∠DAE=90°,
∴∠AED+∠ADE=90°,
∵∠PDA=∠ABD=∠AED,
∴∠PDA+∠ADE=90°,
即PD⊥DO,
∴PD与圆O相切于点D;
(2)∵tan∠ADB=![]()
∴可设AH=3k,则DH=4k,
∵PA=![]() AH,
AH,
∴PA=(4![]() -3)k,
-3)k,
∴PH=4![]() k,
k,
∴在Rt△PDH中,tan∠P=![]() ,
,
∴∠P=30°,∠PDH=60°,
∵PD⊥DO,
∴∠BDE=90°-∠PDH=30°,
连接BE,则∠DBE=90°,DE=2r=50,
∴BD=DE![]() cos30°=25
cos30°=25![]()


科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x+6与反比例函数y2=![]() (x<0)的图象相交于点A、B,其中点A的坐标是(-2,4).
(x<0)的图象相交于点A、B,其中点A的坐标是(-2,4).
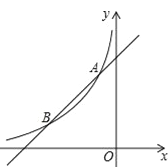
(1)求反比例函数的解析式和点B的坐标;
(2)观察图象,比较当x<0时,y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天数学课上,老师讲了提取公因式分解因式,放学后,小华回到家拿出课堂笔记,认真复习老师课上讲的内容,他突然发现一道题:-12xy2+6x2y+3xy=-3xy(4y-______)横线空格的地方被钢笔水弄污了,你认为横线上应填写( )
A.2xB.-2xC.2x-1D.-2x-l
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市一月份的营业额为200万元,三月份的营业额为288万元,如果每月比上一个月增长的百分数相同,则每月的平均增长率为( )
A.10%
B.15%
C.20%
D.25%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是( )
A. 3 B. 6 C. 9 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB:OE=3:2.其中正确结论的个数是 ( )
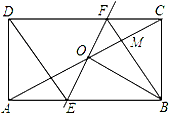
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com