

分析 (1)用D情况的人数除以其占总人数的百分比可得;
(2)用总人数乘以各情况的百分比求得A、B、C的人数即可补全统计图;
(3)用总人数乘以样本中A情况的百分比可得答案.
解答 解:(1)本次活动参与调查的市民人数为15÷15%=100(人),
故答案为:100;
(2)A情况的百分比为1-(20%+60%+15%)=5%,
则A情况的人数为100×5%=5(人),B情况的人数为100×20%=20(人),C情况的人数为100×60%=60(人),
补全条形图如下:
(3)24×5%=1.2(万人),
答:估算每天都用公共自行车的市民有1.2万人.
点评 本题考查了条形统计图,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


科目:初中数学 来源: 题型:解答题
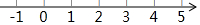 解不等式组$\left\{\begin{array}{l}{\frac{1}{2}x>1,①}\\{1-x≥-3,②}\end{array}\right.$
解不等式组$\left\{\begin{array}{l}{\frac{1}{2}x>1,①}\\{1-x≥-3,②}\end{array}\right.$查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
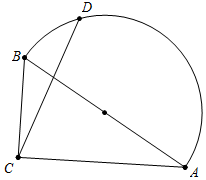 如图,在Rt△ABC中,∠ACB=90°,tan∠CAB=$\frac{\sqrt{3}}{3}$,AB=3,点D在以斜边AB为直径的半圆上,点M是CD的三等分点,当点D沿着半圆,从点A运动到点B时,点M运动的路径长为( )
如图,在Rt△ABC中,∠ACB=90°,tan∠CAB=$\frac{\sqrt{3}}{3}$,AB=3,点D在以斜边AB为直径的半圆上,点M是CD的三等分点,当点D沿着半圆,从点A运动到点B时,点M运动的路径长为( )| A. | π或$\frac{π}{2}$ | B. | $\frac{π}{2}$或$\frac{π}{3}$ | C. | $\frac{π}{3}$或π | D. | $\frac{π}{4}$或$\frac{π}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com