
分析 (1)先将三元一次方程组通过加减消元法转化为二元一次方程组,再通过加减消元法转化为一元一次方程,从而可以解答本题;
(2)先将三元一次方程组通过加减消元法转化为二元一次方程组,再通过加减消元法转化为一元一次方程,从而可以解答本题.
解答 解:(1)$\left\{\begin{array}{l}{x+y+z=26}&{①}\\{x-y=1}&{②}\\{2x-y+z=18}&{③}\end{array}\right.$,
③-①,得x-2y=-8④,
②-④,得y=9,
将y=9代入②,得x=10,
将x=10,y=9代入①,得z=7.
故原方程组的解是$\left\{\begin{array}{l}{x=10}\\{y=9}\\{z=7}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x+4y+3z=9}&{①}\\{3x-2y+5z=11}&{②}\\{5x-6y+7z=13}&{③}\end{array}\right.$,
①+②×2,得8x+13z=31④,
②×3-③,得4x+8z=20⑤,
⑤×2-④,得3z=9,
解得z=3,
将z=3代入⑤,得x=-1,
将x=-1,z=3代入①,得y=$\frac{1}{2}$.
故原方程组的解是$\left\{\begin{array}{l}{x=-1}\\{y=\frac{1}{2}}\\{z=3}\end{array}\right.$.
点评 本题考查解三元一次方程组,解题的关键是利用加减消元法将方程组转化为一元一次方程进行解答.


科目:初中数学 来源: 题型:解答题
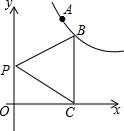 已知点A(1,2)、点B在双曲线y=$\frac{k}{x}$(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点
已知点A(1,2)、点B在双曲线y=$\frac{k}{x}$(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点查看答案和解析>>
科目:初中数学 来源: 题型:填空题
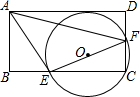 如图,矩形ABCD中,E为BC上一点,F为CD上一点,已知∠AEF=90°,$\frac{AE}{EF}$=$\frac{3}{4}$,△ECF的外接圆与AD相切,则tan∠DAF=$\frac{16}{63}$.
如图,矩形ABCD中,E为BC上一点,F为CD上一点,已知∠AEF=90°,$\frac{AE}{EF}$=$\frac{3}{4}$,△ECF的外接圆与AD相切,则tan∠DAF=$\frac{16}{63}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车匀速行驶(汽车速度大于摩托车的速度);甲先到达B地停留半个小时后返回A地,如图是他们之间的距离y(千米)与甲出发时间x(小时)之间的函数图象,其中D表示甲返回到A地.
甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车匀速行驶(汽车速度大于摩托车的速度);甲先到达B地停留半个小时后返回A地,如图是他们之间的距离y(千米)与甲出发时间x(小时)之间的函数图象,其中D表示甲返回到A地.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com