
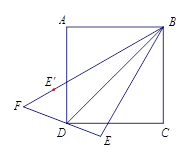
����Ŀ����ͼ���ı��� ![]() �������Σ�
�������� ![]() ��
�� ![]() ��ֱƽ�����ϵĵ㣬��
��ֱƽ�����ϵĵ㣬�� ![]() ����
���� ![]() �ĶԳƵ���
�ĶԳƵ��� ![]() ��ֱ��
��ֱ�� ![]() ��ֱ��
��ֱ�� ![]() ���ڵ�
���ڵ� ![]() .
.
��1������ ![]() ��
�� ![]() �ߵ��е㣬����
�ߵ��е㣬���� ![]() ����
���� ![]() ����
����
��2��С������ʦ�����˽��ֻҪ�� ![]() ���������ε����ģ���ֱ��
���������ε����ģ���ֱ�� ![]() ��
�� ![]() ������Dz��䣮�����Ըı��
������Dz��䣮�����Ըı�� ![]() ��λ�ã�������Ӧ�Ƕȣ���֤��ʦ��˵����
��λ�ã�������Ӧ�Ƕȣ���֤��ʦ��˵����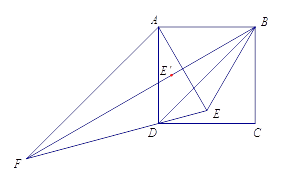
��ͼ������ ![]() ѡ���������ڣ��ҡ�
ѡ���������ڣ��ҡ� ![]() Ϊ�ȱ������Σ����ֱ��
Ϊ�ȱ������Σ����ֱ�� ![]() ��
�� ![]() ������ǵĶ�����
������ǵĶ�����
��3����������о�������⣬��������С�����뷨��Ҳ������������.
��ѡ��С�����뷨����������ֱ�� ![]() ��
�� ![]() ������Ƕ�����˼·��
������Ƕ�����˼·��
���𰸡�
��1��45
��2��
�⣺�� ![]() �ǵȱ������Σ�
�ǵȱ������Σ�
�� ![]() ��
�� ![]() ��
��
���ı��� ![]() �������Σ�
��������
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
�� ![]() ��
�� ![]() ��
��
�� ![]() ��
��
�ߵ� ![]() �ǵ�
�ǵ� ![]() ����
���� ![]() �ĶԳƵ㣬
�ĶԳƵ㣬
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
�� ![]()
�� ![]() ��
��
�� ![]() ��
��
�� ![]()
��3��
�⣺�������С�����뷨��
����һ����ͼ���ҽ��� ![]() ѡ��
ѡ�� ![]() �ߵ��е㣮
�ߵ��е㣮
���ı��� ![]() �������Σ�
��������
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
�ߵ� ![]() �ǵ�
�ǵ� ![]() ����
���� ![]() �ĶԳƵ㣬
�ĶԳƵ㣬
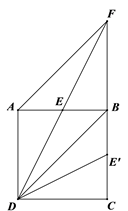
�� ![]() .
.
�� ![]() .
.
�� ![]() ��
�� ![]() ��.
��.
�� ![]() ��ֱ��
��ֱ�� ![]() ��.
��.
�� ![]() .
.
�� ![]() ��
�� ![]() .
.
�� ![]() ��
�� ![]() ���е㣬
���е㣬
�� ![]() ��
��
�� ![]() ��
�� ![]() ��
��
�� ![]() .
.
�� ![]() .
.
�� ![]() ��
��
�� ![]() �ǵ���ֱ��������.
�ǵ���ֱ��������.
�� ![]() .
.
�� ![]() .
.
��ֱ�� ![]() ��
�� ![]() �������Ϊ
�������Ϊ ![]() ��
��
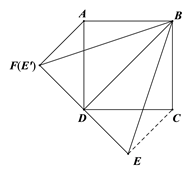
����������ͼ���ҽ��� ![]() ѡ���������⣬ʹ
ѡ���������⣬ʹ ![]() ��λ�ã�
��λ�ã�
���� ![]() ��
��
���ı��� ![]() �������Σ�
��������
�� ![]() ��
�� ![]() ��
��
�� ![]() ��
�� ![]() �Ĵ�ֱƽ�����ϣ�
�Ĵ�ֱƽ�����ϣ�
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
�� ![]() ��
��
�� ![]() ��
��
�ߵ� ![]() �ǵ�
�ǵ� ![]() ����
���� ![]() �ĶԳƵ㣬
�ĶԳƵ㣬
�� ![]() ��
��
�� ![]() ��
�� ![]() ��
�� ![]() ���㹲��.
���㹲��.
��� ![]() ���
��� ![]() �غϣ�
�غϣ�
�� ![]() ��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
�� ![]() ��
��
�� ![]() ��
��
����������1��������֪��������ͼ�μ�����á� FAD����.
��2���ɵȱ������ε����ʵ� ��EBA=��EAB=60�� �� BE=EA=AB �������������ʵ� AB=AD �� ��ABD=45�� �� ��BAD=90�� ������������AE=AD�� �� ��EAD=��BAD��BAE=30�� �� ��AED=75�� ��������֤��ABF �� ��EBF������ȫ�������ε����ʵ�FA=FE ����FAE=��FEA=75�� ����FAD=��FAE��EAD=45��
��3���� E ѡ���������⣬ʹ ��EDC=45�� ��λ�ã����� CE ��
�����������ʵã� DA=DC �� ��BDA=��BDC=45�� ����E��ֱƽ���ߵ����ʵ�ED=CE ���ɵ��������ε����ʵ�ED��BD ��������֪����֤
��ADF �� ��CDE �����ݵ��������ε����ʵ� ��FAD=��ECD=45�� .
�����㾫�������յ���ֱ�������κ͵ȱ������ε������ǽ����ĸ�������Ҫ֪������ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣻�ȱ������ε������Ƕ���Ȳ���ÿ���Ƕ���60�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c�ǡ�ABC�����߳����ҷ���a��1+x2��+2bx��c��1��x2��=0��������ȣ����ABCΪ��������
A. ���������� B. ֱ�������� C. �ȱ������� D. ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ��ֱ�����ǰ壨�Ƕȷֱ�Ϊ30�㡢60�㡢90���45�㡢45�㡢90�㣩����ͼ(1)��ʾ������һ�����ǰ��ֱ�DZ�AC��ֱ�����ᣬAC���е������ԭ��O��AC��8��б��AB�������ڵ�G����G��Ӧ�����ϵ�����4����һ�����ǰ��ֱ�DZ�AE�������ڵ�F��б��AD�������ڵ�H��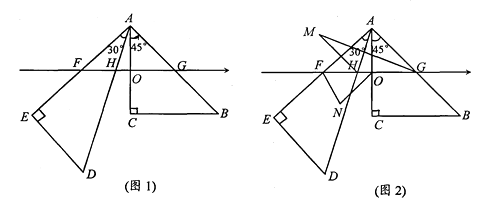
��1�������AGH�������10����AHF�������8�����F��Ӧ�������ϵ����� �� ��H��Ӧ�������ϵ�������
��2����ͼ(2)�����AHF��ƽ���ߺ͡�AGH��ƽ���߽��ڵ�M������HAO��a������a����ʾ��M�Ĵ�С����д���������̣�
��3����ͼ(2)�����AHF��ƽ���ߺ͡�AGH��ƽ���߽��ڵ�M�����EFH��ƽ���ߺ�
��FOC��ƽ���߽��ڵ�N�����N����M��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCO�У�OΪ����ԭ�㣬A��y���ϣ�C��x���ϣ�B������Ϊ��8��6����P���߶�BC�϶��㣬��D��ֱ��y=2x��6�ϵ�һ���ĵ㣬����APD�ǵ���ֱ�������Σ����D������Ϊ_____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2017�����ڷżٰ��죬���ٹ�·���ͨ�У����ط羰��������֯���������������ı����ʹ���10��1�յ��ο��������Ѿ��ﵽ��7���ˣ��������������У�ÿ����ο������仯����λ�����ˣ����±���������ʾ��ǰһ����������������ʾ��ǰһ���ٵ���������
��1��10��3�յ�����Ϊ���ˣ�
��2������죬�ο�����������10���գ��ﵽ���ˣ��ο��������ٵ���10���գ�Ϊ���ˣ�
��3����8��ι۹ʹ���������ԼΪ���ˣ������ȷ����λ��
��4���������һ���˴�������һ������ڲι۹ʹ�����������ǵij���������һ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
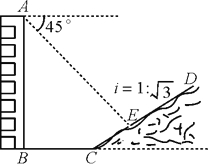
����Ŀ����ͼ��һ¥��AB����һ��ɽ�����¶�Ϊi��1��![]() ��ɽ��������E�㴦��һ��Ϣͤ����
��ɽ��������E�㴦��һ��Ϣͤ����
�ü�ɽ�½�C��¥��ˮƽ����BC��25�ף���ͤ�Ӿ���CE��20�ף�С����¥�������E��ĸ���
Ϊ45������¥��AB�ĸߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Rt��ABC�У�BA=BC����ABC=90�㣬��D��AC�ϣ�����ABD�Ƶ�B��˳ʱ�뷽����ת90��õ���CBE��
��1�����DCE�Ķ�����
��2����AB=4��CD=3AD����DE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�ڣ���C��y��������D�㣬��x���ཻ��A��2��0����B��8��0�����㣬Բ��C�ڵ������ޣ�
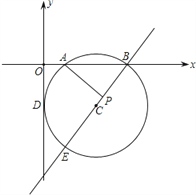
��1�����C�����ꣻ
��2������BC���ӳ�����C����һ��E�����߶�BE����һ��P��ʹ��AB2=BPBE���ܷ��Ƴ�AP��BE���������Ľ��ۣ���˵�����ɣ�
��3����ֱ��BE���Ƿ���ڵ�Q��ʹ��AQ2=BQEQ�������ڣ������Q�����ꣻ�������ڣ�Ҳ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ������CΪ��O��һ�㣬AE����C�������ഹֱ������ΪE��AE����O�ڵ�D��ֱ��EC��AB���ӳ����ڵ�P������AC��BC��PB��PC=1��2��

��1����֤��ACƽ����BAD��
��2��̽���߶�PB��AB֮���������ϵ����˵�����ɣ�
��3����AD=3������ABC�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com