
| A. | 平均数是15 | B. | 众数是10 | C. | 中位数是17 | D. | 方差是$\frac{44}{3}$ |
分析 根据方差、众数、平均数和中位数的计算公式和定义分别进行解答即可.
解答 解:平均数是:(10+15+10+17+18+20)÷6=15,A说法正确,不符合题意;
10出现了2次,出现的次数最多,则众数是10,B说法正确,不符合题意;
把这组数据从小到大排列为10,10,15,17,18,20,
最中间的数是(15+17)÷2=16,则中位数是16,C说法错误,符合题意;
方差是:$\frac{1}{6}$[2(10-15)2+(15-15)2+(17-15)2+(18-15)2+(20-15)2]=$\frac{88}{6}$=$\frac{44}{3}$,D正确,不符合题意.
则下列说法错误的是C.
故选:C.
点评 此题考查了方差、众数、平均数和中位数的定义.用到的知识点:一组数据中出现次数最多的数据叫做这组数据的众数.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.平均数是指在一组数据中所有数据之和再除以数据的个数.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
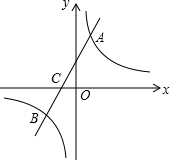 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A,B两点,与x轴交于C点,已知点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A,B两点,与x轴交于C点,已知点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
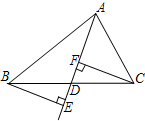 如图,在△ABC中,已知D是边BC上一点,BE⊥AD,CF⊥AD,垂足分别为E,F,且BE=CF,请你判断AD是不是△ABC的中线,如果是,请给出证明,如果不是,请说明理由.
如图,在△ABC中,已知D是边BC上一点,BE⊥AD,CF⊥AD,垂足分别为E,F,且BE=CF,请你判断AD是不是△ABC的中线,如果是,请给出证明,如果不是,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
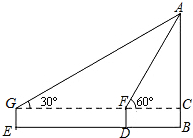 某同学利用测角仪及卷尺测量某校旗杆的高度,在测量中获得了一些数据,并以此画出了如图所示的示意图,已知该同学使用的测角仪(离地面的高度)支杆长1m,第一次在D处测得旗杆顶端A的仰角为60°,第二次向后退12m到达E处,又测到旗杆顶端A的仰角为30°,求旗杆的高度.(结果保留根号)
某同学利用测角仪及卷尺测量某校旗杆的高度,在测量中获得了一些数据,并以此画出了如图所示的示意图,已知该同学使用的测角仪(离地面的高度)支杆长1m,第一次在D处测得旗杆顶端A的仰角为60°,第二次向后退12m到达E处,又测到旗杆顶端A的仰角为30°,求旗杆的高度.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5条 | B. | 6条 | C. | 7条 | D. | 8条 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,⊙O中的弦AB与弦CD交于点P,点M、N分别是AB、CD的中点,$\widehat{AC}$=$\widehat{BD}$,求证:△PMN是等腰三角形.
已知:如图,⊙O中的弦AB与弦CD交于点P,点M、N分别是AB、CD的中点,$\widehat{AC}$=$\widehat{BD}$,求证:△PMN是等腰三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com