
【题目】如图,点![]() 是直线
是直线![]() 与反比例函数
与反比例函数![]() (
(![]() 为常数)的图象的交点.过点
为常数)的图象的交点.过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,且
,且![]() .
.
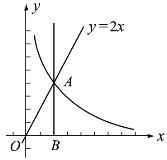
(1)求点![]() 的坐标及
的坐标及![]() 的值;
的值;
(2)已知点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交直线
轴的直线,交直线![]() 于点
于点![]() ,交反比例函数
,交反比例函数![]() (
(![]() 为常数)的图象于点
为常数)的图象于点![]() ,交垂线
,交垂线![]() 于点
于点![]() .若
.若![]() ,结合函数的图象,直接写出
,结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)A(2,4);m=9;(2)6<x1+x2+x3≤7
【解析】
(1)由点A在正比例函数y=2x的图象上,可得点A的坐标为(2,4),再根据点A在反比例函数![]() 的图象上,即可得出m的值;
的图象上,即可得出m的值;
(2)依据x2<x3<x1,结合函数的图象,即可写出x1+x2+x3的取值范围.
解:(1)由题意得,可知点A的横坐标是2,
由点A在正比例函数y=2x的图象上,
∴点A的坐标为(2,4),
又∵点A在反比例函数![]() 的图象上,
的图象上,
∴4=![]() ,
,
即m=9;
(2)∵过点P(0,n)作平行于x轴的直线,交直线y=2x于点C(x1,y1),交反比例函数![]() (m为常数)的图象于点D(x2,y2),交垂线AB于点E(x3,y3),而x2<x3<x1,
(m为常数)的图象于点D(x2,y2),交垂线AB于点E(x3,y3),而x2<x3<x1,
∴4<n≤8,
∵当n=4时,x1+x2+x3=2+2+2=6;当n=8时,x1+x2+x3=4+1+2=7,
∴6<x1+x2+x3≤7.


科目:初中数学 来源: 题型:
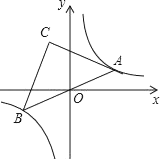
【题目】如图,点A是双曲线y=![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为_____.
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个箱子内有3颗相同的球,将3颗球分别标示号码1,2,5,今浩浩以每次从箱子内取一颗球且取后放回的方式抽取,并预计取球10次,现已取了8次,取出的结果依次为1,2,2,5,5,2,1,2,若每次取球时,任一颗球被取到的机会皆相等,且取出的号码即为得分数,浩浩打算依计划继续从箱子取球2次,则发生“这10次得分的平均数在2.2~2.4之间(含2.2,2.4)”的情形的概率为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知将抛物线![]() 沿
沿![]() 轴向上翻折与所得抛物线围成一个封闭区域(包括边界),在这个区域内有5个整点(点
轴向上翻折与所得抛物线围成一个封闭区域(包括边界),在这个区域内有5个整点(点![]() 满足横、纵坐标都为整数,则把点
满足横、纵坐标都为整数,则把点![]() 叫做“整点”).现将抛物线
叫做“整点”).现将抛物线![]() 沿
沿![]() 轴向下翻折,所得抛物线与原抛物线所围成的封闭区域内(包括边界)恰有11个整点,则
轴向下翻折,所得抛物线与原抛物线所围成的封闭区域内(包括边界)恰有11个整点,则![]() 的取值范围是( )
的取值范围是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了解旅游人数的变化情况,收集并整理了2017年1月至2019年12月期间的月接待旅游量(单位:万人次)的数据并绘制了统计图如下:
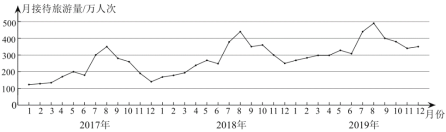
根据统计图提供的信息,下列推断不合理的是( )
A.2017年至2019年,各年的月接待旅游量高峰期大致在7,8月份
B.2019年的月接待旅游量的平均值超过300万人次
C.2017年至2019年,年接待旅游量逐年增加
D.2017年至2019年,各年下半年(7月至12月)的月接待旅游量相对于上半年(1月至6月)波动性更小,变化比较平稳
查看答案和解析>>
科目:初中数学 来源: 题型:
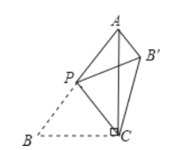
【题目】如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合)将△BCP沿CP所在的直线翻折,得到![]() ,连接
,连接![]() ,下面有四个判断:
,下面有四个判断:
①当AP=BP时,![]() ∥CP;
∥CP;
②当AP=BP时,![]()
③当CP⊥AB时,![]() ;
;
④![]() 长度的最小值是1.
长度的最小值是1.
所有正确结论的序号是( )
A.①③④B.①②C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是圆上一点,点D是半圆的中点,连接CD交OB于点E,点F是AB延长线上一点,CF=EF.
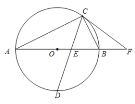
(1)求证:FC是⊙O的切线;
(2)若CF=5,![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,对称轴与
两点,对称轴与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 是平面内一动点,且满足
是平面内一动点,且满足![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() .则线段
.则线段![]() 的最大值是________________.
的最大值是________________.
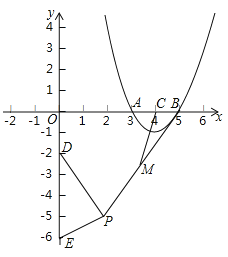
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,反比例函数
,反比例函数![]() 在第一象限内的图象分别交
在第一象限内的图象分别交![]() ,
,![]() 于点
于点![]() 和点
和点![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)求反比例函数解析式;
(3)求点![]() 的坐标.
的坐标.
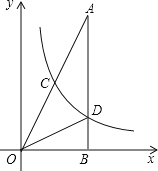
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com