
【题目】如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2=_____.

【答案】45°
【解析】
如图,连接AC,BC,根据勾股定理及其逆定理,求得∠ACB=90°,∠CAB=45°.再证明四边形ADFC是平行四边形,可得AC∥DF,根据两直线平行,同位角相等可得∠2=∠DAC,在Rt△ABD中,∠1+∠DAB=90°,又因∠DAB=∠DAC+∠CAB,所以∠1+∠CAB+∠DAC=90°,即可得∠1+∠DAC=45°,即∠1+∠2=∠1+∠DAC=45°.
如图,连接AC,BC.

根据勾股定理,AC=BC=![]() ,AB=
,AB=![]() .
.
∵(![]() )2+(
)2+(![]() )2=(
)2=(![]() )2,
)2,
∴∠ACB=90°,∠CAB=45°.
∵AD∥CF,AD=CF,
∴四边形ADFC是平行四边形,
∴AC∥DF,
∴∠2=∠DAC(两直线平行,同位角相等),
在Rt△ABD中,
∠1+∠DAB=90°(直角三角形中的两个锐角互余);
又∵∠DAB=∠DAC+∠CAB,
∴∠1+∠CAB+∠DAC=90°,
∴∠1+∠DAC=45°,
∴∠1+∠2=∠1+∠DAC=45°.
故答案为:45°.


科目:初中数学 来源: 题型:
【题目】如图,在等腰RtABC 中,∠BAC=90°,在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连接PC,若△ABC的面积为8cm2,则△BPC的面积为( )

A. 4cm2 B. 5cm2 C. 6cm2 D. 7cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( ) 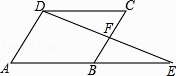
A.∠E=∠CDF
B.EF=DF
C.AD=2BF
D.BE=2CF
查看答案和解析>>
科目:初中数学 来源: 题型:
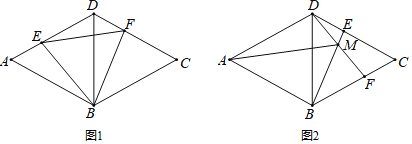
【题目】如图,已知菱形ABCD边长为4,![]() ,点E从点A出发沿着AD、DC方向运动,同时点F从点D出发以相同的速度沿着DC、CB的方向运动.
,点E从点A出发沿着AD、DC方向运动,同时点F从点D出发以相同的速度沿着DC、CB的方向运动.
![]() 如图1,当点E在AD上时,连接BE、BF,试探究BE与BF的数量关系,并证明你的结论;
如图1,当点E在AD上时,连接BE、BF,试探究BE与BF的数量关系,并证明你的结论;
![]() 在
在![]() 的前提下,求EF的最小值和此时
的前提下,求EF的最小值和此时![]() 的面积;
的面积;
![]() 当点E运动到DC边上时,如图2,连接BE、DF,交点为点M,连接AM,则
当点E运动到DC边上时,如图2,连接BE、DF,交点为点M,连接AM,则![]() 大小是否变化?请说明理由.
大小是否变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E. 
(1)求证:CE是⊙O的切线;
(2)若AE=1,CE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
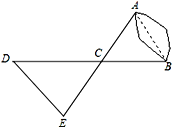
【题目】如图,A、B两点分别位于一个池塘的两侧,池塘西边有一座假山D,在DB的中点C处有一个雕塑,小川从点A出发,沿直线AC一直向前经过点C走到点E,并使CE=CA,然后他测量点E到假山D的距离,则DE的长度就是A、B两点之间的距离.
(1)你能说明小川这样做的根据吗?
(2)如果小川恰好未带测量工具,但是知道A和假山D、雕塑C分别相距200米、120米,你能帮助他确定AB的长度范围吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A、B两点,与双曲线y2= ![]() (x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论: ①当x>0时,y1随x的增大而增大,y2随x的增大而减小;
(x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论: ①当x>0时,y1随x的增大而增大,y2随x的增大而减小;
②k=4;
③当0<x<2时,y1<y2;
④如图,当x=4时,EF=4.
其中正确结论的个数是( )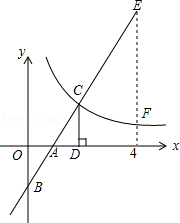
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平移线段AB,使点A移动到点A1.
(1)画出平移后的线段A1B1,分别连接AA1,BB1.
(2)分别画出AC⊥A1B1于点C,AD⊥BB1于点D.
(3)AA1与BB1之间的距离,就是线段 的长度.
(4)线段AB平移的距离,就是线段 的长度.
(5)线段BD的长度,是点B到直线 的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com