
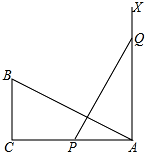
 如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP=6或12.
如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP=6或12. 分析 本题要分情况讨论:①Rt△APQ≌Rt△CBA,此时AP=BC=6,可据此求出P点的位置.②Rt△QAP≌Rt△BCA,此时AP=AC=12,P、C重合.
解答 解:①当AP=CB时,
∵∠C=∠QAP=90°,
在Rt△ABC与Rt△QPA中,$\left\{\begin{array}{l}{AP=CB}\\{AB=QP}\end{array}\right.$,
∴Rt△ABC≌Rt△QPA(HL),
即AP=BC=6;
②当P运动到与C点重合时,AP=AC,
在Rt△ABC与Rt△QPA中,$\left\{\begin{array}{l}{AP=AC}\\{QP=AB}\end{array}\right.$,
∴Rt△QAP≌Rt△BCA(HL),
即AP=AC=12,
∴当点P与点C重合时,△ABC才能和△APQ全等.
综上所述,AP=6或12.
故答案为:6或12.
点评 本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.由于本题没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{y}{{x}^{2}}$$÷\frac{(-y)^{2}}{x}$=$\frac{1}{xy}$ | |
| B. | ($\frac{3x}{-2y}$)2$•(\frac{2y}{-3x})$3=-$\frac{2y}{3x}$ | |
| C. | $\frac{xy}{{x}^{2}-2xy+{y}^{2}}$$÷\frac{x{y}^{2}+{x}^{2}y}{{x}^{2}-{y}^{2}}$=$\frac{1}{x-y}$ | |
| D. | $\frac{{x}^{2}+x}{{x}^{2}+2x+1}$$•\frac{{x}^{2}-1}{x-1}$=x(x+1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com