
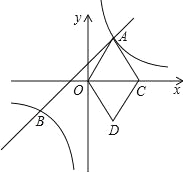
【题目】如图,在平面直角坐标系xOy中,直线y=mx+1与双曲y=![]() (k>0)相交于点A、B,点C在x轴正半轴上,点D(1,﹣2),连结OA、OD、DC、AC,四边形AODC为菱形.
(k>0)相交于点A、B,点C在x轴正半轴上,点D(1,﹣2),连结OA、OD、DC、AC,四边形AODC为菱形.
(1)求k和m的值;
(2)根据图象写出反比例函数的值小于2时x的取值范围;
(3)设点P是y轴上一动点,且![]() ,求点P的坐标.
,求点P的坐标.
【答案】(1)m=1;k=2;(2)x<0或x>1;;(3)(0,8)或(0,﹣8).
【解析】
试题分析:(1)由菱形的性质可知A、D关于x轴对称,可求得A点坐标,把A点坐标分别代入两函数函数解析式可求得k和m值;
(2)由(1)可知A点坐标为(1,2),结合图象可知在A点的下方时,反比例函数的值小于2,可求得x的取值范围;
(3)根据菱形的性质可求得C点坐标,可求得菱形面积,设P点坐标为(0,y),根据条件可得到关于y的方程,可求得P点坐标.
试题解析:(1)如图,连接AD,交x轴于点E,
∵D(1,2),
∴OE=1,ED=2,
∵四边形AODC是菱形,
∴AE=DE=2,EC=OE=1,
∴A(1,2),
将A(1,2)代入直线y=mx+1可得m+1=2,解得m=1,
将A(1,2)代入反比例函数y=![]() ,可求得k=2;
,可求得k=2;

(2)∵当x=1时,反比例函数的值为2,
∴当反比例函数图象在A点下方时,对应的函数值小于2,
此时x的取值范围为:x<0或x>1;
(3)∵OC=2OE=2,AD=2DE=4,
∴![]() =
=![]() OCAD=4,
OCAD=4,
∵![]() ,
,
∴![]() =4,
=4,
设P点坐标为(0,y),则OP=|y|,
∴![]() ×|y|×1=4,即|y|=8,
×|y|×1=4,即|y|=8,
解得y=8或y=﹣8,
∴P点坐标为(0,8)或(0,﹣8).


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】计算(3a2-2a+1)-(2a2+3a-5)的结果是( )
A. a2-5a+6 B. 7a2-5a-4 C. a2+a-4 D. a2+a+6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四边形的周长是48厘米,已知第一条边长a厘米,第二条边比第一条边的2倍长3厘米,第三条边等于第一、二两条边的和,写出表示第四条边长的整式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架2.5米长的梯子斜立在竖直的墙上,此时梯足B距底端O为0.7米。(1)求OA的长度。(2)如果梯子顶端下滑0.4米,则梯子将滑出多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第1个等式:![]() ; 第2个等式:
; 第2个等式:![]() ;
;
第3个等式:![]() ; 第4个等式:
; 第4个等式:![]() ;…
;…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= .
(2)用含有n的代数式表示第n个等式:an=(n为正整数)
(3)求a1+a2+a3+a4+…+a100的值.
(4)探究计算:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com