
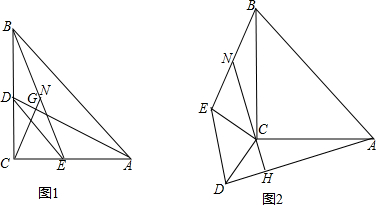
���� ��1������ֱ�������ε����ʵõ�BE=2CN=17�����ݹ��ɶ����õ�BC=$\sqrt{B{E}^{2}-C{E}^{2}}$=15�����ɵõ����ۣ�
��2��������֪�����Ƴ���ACD�ա�BCE������ȫ�������ε����ʵõ���CAD=��CBE����ֱ�������ε����ʵõ�CN=BN�����ݵ��������ε����ʵõ���CBE=��NCD�����������õ���NCD=��CAD�����ɵõ����ۣ�
��3����ͼ2���ӳ�CN��FʹFN=CN������BF��ͨ��֤����CEN�ա�BNF���õ�CE=BF����F=��ECN���Ƴ���CBF=��DCA��֤�á�ACD�ա�BCF������ȫ�������ε����ʵõ���DAC=��BCF�������������ɵõ����ۣ�
��� �⣺��1���ߡ�ACB=90�㣬��N���߶�BE���е㣬
��BE=2CN=17��
��CE=8��
��BC=$\sqrt{B{E}^{2}-C{E}^{2}}$=15��
��CD=CE=8��
��BD=BC-CD=7��
��S��BDE=BD•CE•$\frac{1}{2}$=7��8��$\frac{1}{2}$=28��
��2���ڡ�ACD���BCE�У�
$\left\{\begin{array}{l}{AC=BC}\\{��ACD=��BCE}\\{CD=CE}\end{array}\right.$��
���ACD�ա�BCE��
���CAD=��CBE��
�ߡ�ACB=90�㣬��N���߶�BE���е㣬
��CN=BN��
���CBE=��NCD��
���NCD=��CAD��
�ߡ�NCD+��NCA=90�㣬
���CAG+��GCA=90�㣬
���CGA=90�㣬
��CN��AD��
��3����2���еĽ��ۻ���������ͼ2���ӳ�CN��FʹFN=CN������BF��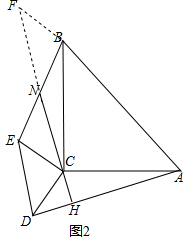
�ڡ�CEN���BFN�У�
$\left\{\begin{array}{l}{CN=FN}\\{��CNE=��BNF}\\{EN=BN}\end{array}\right.$��
���CEN�ա�BNF��
��CE=BF����F=��ECN
�ߡ�CBF=180��-��F-��BCF����DCA=360��-��DCE-��ACB-��BCE=180��-��ECF-��BCF��
���CBF=��DCA��
��CE=CD��
��BF=CD��
�ڡ�ACD���BCF�У�
$\left\{\begin{array}{l}{CD=BF}\\{��ACD=��FBC}\\{AC=BC}\end{array}\right.$��
���ACD�ա�BCF��
���DAC=��BCF��
�ߡ�BCF+��ACH=90�㣬
���CAH+��ACH=90�㣬
���AHC=90�㣬
��CN��AD��
���� ���⿼����ȫ�������ε��ж������ʣ�����ֱ�������ε����ʣ������ε������ʽ����ȷ�������������ǽ���Ĺؼ���


 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����������ȵ�ʵ���� | B�� | ��������ȵ�ʵ���� | ||
| C�� | ����ֻ��һ��ʵ���� | D�� | û��ʵ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
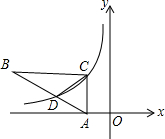 ��ͼRt��ABC��ƽ������ϵ�У�����A��x���ϣ���ACB=90�㣬CB��x�ᣬ˫����y=$\frac{k}{x}$����C�㼰AB�����ȵ�D��BD=2AD����S��BCD=6����k��ֵΪ��������
��ͼRt��ABC��ƽ������ϵ�У�����A��x���ϣ���ACB=90�㣬CB��x�ᣬ˫����y=$\frac{k}{x}$����C�㼰AB�����ȵ�D��BD=2AD����S��BCD=6����k��ֵΪ��������| A�� | 3 | B�� | 6 | C�� | -3 | D�� | -6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �˽�ijУ�ţ�1����ѧ��������� | B�� | ����2016�����Ӵ����������� | ||
| C�� | ���һ������ݵ�ʹ������ | D�� | �˽�������ѧ����������ʱ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����4��4�����������У���ѡȡһ����ɫ��С�����β�Ϳ�ڣ�ʹͼ�к�ɫ���ֵ�ͼ�ι���һ����Գ�ͼ�εĸ����ǣ�������
��ͼ����4��4�����������У���ѡȡһ����ɫ��С�����β�Ϳ�ڣ�ʹͼ�к�ɫ���ֵ�ͼ�ι���һ����Գ�ͼ�εĸ����ǣ�������| A�� | $\frac{6}{13}$ | B�� | $\frac{5}{13}$ | C�� | $\frac{4}{13}$ | D�� | $\frac{3}{13}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{4}=��2$ | B�� | ��-1��2016=-1 | C�� | ��-3��-2=6 | D�� | ��-2��3�£�-2��2=-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��1 | B�� | x��1 | C�� | x��-2 | D�� | -2��x��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
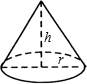 ��ͼ��Բ�ĵ���뾶rΪ6cm����hΪ8cm����Բ�IJ����Ϊ��������
��ͼ��Բ�ĵ���뾶rΪ6cm����hΪ8cm����Բ�IJ����Ϊ��������| A�� | 30��cm2 | B�� | 48��cm2 | C�� | 60��cm2 | D�� | 80��cm2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com