下列说法中:
①已知D是△ABC中的边BC上的一点,∠BAD=∠C,则有AB2=BD•BC;
②若关于x的不等式2x-m<0有且只有一个正整数解,则m的取值范围是2<m≤4;
③在一个有12000人的小镇上,随机抽样调查2000人,其中有360人看过“7•23甬温线特别重大铁路交通事故”新闻报道.那么在该镇随便问一人,他(她)看过央视这一报道的概率是18%;
④如果直角三角形的斜边长为18,那么这个直角三角形的三条边上的中线的交点到直角顶点的距离为6.正确命题有( )
A.1个
B.2个
C.3个
D.4个
【答案】
分析:①利用相似三角形的判定定理以及相似三角形的对应边的比相等,即可判断;
②根据不等式的解集的确定方法即可确定m的范围;
③根据总体概率约等于样本概率,即可求得;
④根据直角三角形斜边上的中线等于斜边的一半,以及三角形的重心的性质即可判断.
解答:解:①∵∠BAD=∠C,且∠B=∠B,
∴△ABC∽△DBA
∴
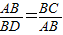
,
∴AB
2=BD•BC,故命题正确;
②解不等式2x-m<0,得:x<
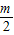
,
∵不等式2x-m<0有且只有一个正整数解,
∴1<
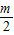
≤2,
则2<m≤4,故命题正确;
③随机抽样调查2000人,其中有360人看过“7•23甬温线特别重大铁路交通事故”新闻报道.那么在该镇随便问一人,他(她)看过央视这一报道的概率是18%,正确;
④直角三角形的斜边长为18,则斜边上的中线长是

×18=9,则三条边上的中线的交点到直角顶点的距离为9×

=6,故命题正确.
故选D.
点评:主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.

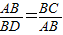 ,
,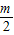 ,
,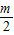 ≤2,
≤2, ×18=9,则三条边上的中线的交点到直角顶点的距离为9×
×18=9,则三条边上的中线的交点到直角顶点的距离为9× =6,故命题正确.
=6,故命题正确.
