
| A. | $\frac{\sqrt{3}}{8}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{8}$ |
分析 由于内接正三角形、正方形、正六边形是特殊内角的多边形,可构造直角三角形分别求出边心距的长,由勾股定理逆定理可得该三角形是直角三角形,进而可得其面积.
解答 解:如图1,
∵OC=1,
∴OD=1×sin30°=$\frac{1}{2}$;
如图2,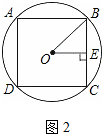
∵OB=1,
∴OE=1×sin45°=$\frac{\sqrt{2}}{2}$;
如图3,
∵OA=1,
∴OD=1×cos30°=$\frac{\sqrt{3}}{2}$,
则该三角形的三边分别为:$\frac{1}{2}$、$\frac{\sqrt{2}}{2}$、$\frac{\sqrt{3}}{2}$,
∵($\frac{1}{2}$)2+($\frac{\sqrt{2}}{2}$)2=($\frac{\sqrt{3}}{2}$)2,
∴该三角形是以$\frac{1}{2}$、$\frac{\sqrt{2}}{2}$为直角边,$\frac{\sqrt{3}}{2}$为斜边的直角三角形,
∴该三角形的面积是$\frac{1}{2}$×$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{8}$,
故选:D.
点评 本题主要考查多边形与圆,解答此题要明确:多边形的半径、边心距、中心角等概念,根据解直角三角形的知识解答是解题的关键.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案科目:初中数学 来源: 题型:解答题
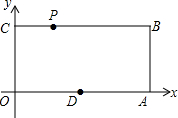 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
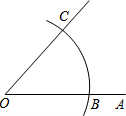 如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为( )
如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
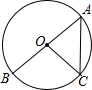 如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则$\widehat{BC}$的长为( )
如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则$\widehat{BC}$的长为( )| A. | $\frac{10}{3}$π | B. | $\frac{10}{9}$π | C. | $\frac{5}{9}$π | D. | $\frac{5}{18}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
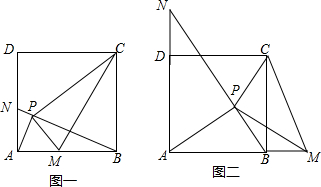
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
如图,四边形ABCD内接于⊙O,F是$\widehat{CD}$上一点,且$\widehat{DF}$=$\widehat{BC}$,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线a∥b,直线l分别与直线a,b相交于点P,Q,PM垂直于l,若∠1=58°,则∠2的度数为( )
如图,直线a∥b,直线l分别与直线a,b相交于点P,Q,PM垂直于l,若∠1=58°,则∠2的度数为( )| A. | 58° | B. | 90° | C. | 32° | D. | 38° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
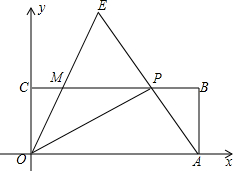 如图,在直角坐标系xOy中,矩形OABC的顶点A、C分别在x轴和y轴正半轴上,点B的坐标是(5,2),点P是CB边上一动点(不与点C、点B重合),连结OP、AP,过点O作射线OE交AP的延长线于点E,交CB边于点M,且∠AOP=∠COM,令CP=x,MP=y.
如图,在直角坐标系xOy中,矩形OABC的顶点A、C分别在x轴和y轴正半轴上,点B的坐标是(5,2),点P是CB边上一动点(不与点C、点B重合),连结OP、AP,过点O作射线OE交AP的延长线于点E,交CB边于点M,且∠AOP=∠COM,令CP=x,MP=y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com