
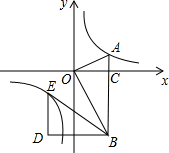
 ��ͼ����ƽ��ֱ������ϵ�У�OA��OB��AB��x���ڵ�C����A��$\sqrt{3}$��1���ڷ���������y=$\frac{k}{x}$��ͼ���ϣ�
��ͼ����ƽ��ֱ������ϵ�У�OA��OB��AB��x���ڵ�C����A��$\sqrt{3}$��1���ڷ���������y=$\frac{k}{x}$��ͼ���ϣ����� ��1���ɵ�A�����꣬���ô���ϵ��������÷�������������ʽ��
��2������������á�A=��COB���������Ǻ����Ķ���ɵõ�OC2=AC•BC�������BC�ij�������á�AOB���������P������Ϊ��m��0����������ɵõ�����m�ķ��̣������m��ֵ��
��3������������á�ABD=90�㣬��BD��x�ᣬ��BD��DE�ij��������E�����꣬���뷴������������ʽ�����жϼ��ɣ�
��� �⣺
��1���ߵ�A��$\sqrt{3}$��1���ڷ���������y=$\frac{k}{x}$��ͼ���ϣ�
��k=$\sqrt{3}$��1=$\sqrt{3}$��
�෴������������ʽΪy=$\frac{\sqrt{3}}{x}$��
��2����A��$\sqrt{3}$��1����AB��x���ڵ�C��
��OC=$\sqrt{3}$��AC=1��
��OA��OB��OC��AB��
���A=��COB��
��tan��A=$\frac{OC}{AC}$=tan��COB=$\frac{CB}{OC}$��
��OC2=AC•BC����BC=3��
��AB=4��
��S��AOB=$\frac{1}{2}$��$\sqrt{3}$��4=2$\sqrt{3}$��
��S��AOP=$\frac{1}{2}$S��AOB=$\sqrt{3}$��
���P��������m��0����
��$\frac{1}{2}$��|m|��1=$\sqrt{3}$�����|m|=2$\sqrt{3}$��
��P��x��ĸ������ϵĵ㣬
��m=-2$\sqrt{3}$��
���P��������-2$\sqrt{3}$��0����
��3���ɣ�2����֪tan��COB=$\frac{CB}{OC}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$��
���COB=60�㣬
���ABO=30�㣬
�߽���BOA�Ƶ�B����ʱ�뷽����ת60��õ���BDE��
���OBD=60�㣬
���ABD=90�㣬
��BD��x�ᣬ
��Rt��AOB�У�AB=4����ABO=30�㣬
��AO=DE=2��OB=DB=2$\sqrt{3}$����BC=3��OC=$\sqrt{3}$��
��OD=DB-OC=$\sqrt{3}$��BC-DE=1��
��E��-$\sqrt{3}$��-1����
��-$\sqrt{3}$����-1��=$\sqrt{3}$��
���E�ڸ÷���������ͼ���ϣ�
���� ����Ϊ�������������ۺ�Ӧ�ã��漰����ϵ�����������ε���������Ǻ����Ķ��塢���ɶ�������ת�����ʵ�֪ʶ���ڣ�1����ע�����ϵ������Ӧ�ã��ڣ�2������á�AOP������ǽ���Ĺؼ����ڣ�3�������BD��AB�ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��һ��ֱ��������ֽƬABO��������ƽ��ֱ������ϵ�У���A��$\sqrt{3}$��0������B��0��3������O��0��0��
��һ��ֱ��������ֽƬABO��������ƽ��ֱ������ϵ�У���A��$\sqrt{3}$��0������B��0��3������O��0��0���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�ȱ�������ABC�ڽ���Բ����P��Բ������һ�㣨P����A��B��C�غϣ������APB=60���120�㣮
��ͼ�ȱ�������ABC�ڽ���Բ����P��Բ������һ�㣨P����A��B��C�غϣ������APB=60���120�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ijУ����ѧ����ѧ��ʽ��һ�γ��������������Ƴ�һ��δ��ɵ�����ͳ��ͼ������У����ѧ��1000�ˣ�����ݴ˹��Ʋ�����ѧ����400�ˣ�
��ͼ��ijУ����ѧ����ѧ��ʽ��һ�γ��������������Ƴ�һ��δ��ɵ�����ͳ��ͼ������У����ѧ��1000�ˣ�����ݴ˹��Ʋ�����ѧ����400�ˣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com