
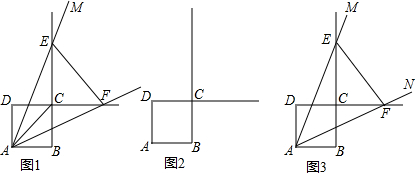
分析 (1)当∠EAF被对角线AC平分时,易证△ACF≌△ACE,因此CF=CE.
(2)①分两种情况进行计算,先用勾股定理得出CF2=8(CE+4)①,再用相似三角形得出4CF=CE(CE+4)②,两式联立解方程组即可;
②先判断出∠AFD=∠CEF,再判断出AF=EF,从而得到△ADF≌△FCE即可.
解答 解:(1)∵四边形ABCD是正方形,
∴∠BCF=∠DCE=90°
∵AC是正方形ABCD的对角线,
∴∠ACB=∠ACD=45°,
∴∠ACF=∠ACE,
∵∠EAF被对角线AC平分,
∴∠CAF=∠CAE,
在△ACF和△ACE中,$\left\{\begin{array}{l}{∠ACF=∠ACE}\\{AC=AC}\\{∠CAF=∠CAE}\end{array}\right.$,
∴△ACF≌△ACE,
∴CF=CE,
(2)当△AEF是直角三角形时,
Ⅰ、当∠AFE=90°时,∴∠AFD+∠CFE=90°,
∵∠CEF+∠CFE=90°,
∴∠AFD=∠CEF
∵∠AFE=90°,∠EAF=45°,
∴∠AEF=45°=∠EAF
∴AF=EF,
在△ADF和△FCE中 $\left\{\begin{array}{l}{∠ADF=∠FCE}\\{∠AFD=∠CEF}\\{AF=EF}\end{array}\right.$,
∴△ADF≌△FCE,
∴FC=AD=2,CE=DF=CD+FC=4,
∴a=4,b=2
Ⅱ、当∠AEF=90°时,
同①的方法得,CF=4,CE=2,
∴a=2,b=4.
(3)ab=8,
理由:
∵AB∥CD
∴∠BAG=∠AFC,
∵∠BAC=45°,
∴∠BAG+∠CAF=45°,
∴∠AFC+∠CAF=45°,
∵∠AFC+∠AEC=180°-(∠CFE+∠CEF)-∠EAF=180°-90°-45°=45°,
∴∠CAF=∠AEC,
∵∠ACF=∠ACE=135°,
∴△ACF∽△ECA,
∴$\frac{AC}{EC}=\frac{CF}{AC}$,
∴EC×CF=AC2=2AB2=2×4=8
∴ab=8.
点评 此题是四边形综合题,主要考查了全等三角形的判定和性质,直角三角形的性质,相似三角形的性质和判定,解本题的关键是判断△ACF∽△ECA,也是本题的难点.


科目:初中数学 来源: 题型:填空题
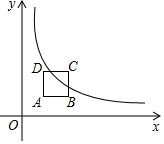 在平面直角坐标系的第一象限内,边长为1的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a),如图,双曲线y=$\frac{3}{x}$(x>0)与此正方形的边有交点,则a的取值范围是$\sqrt{3}$-1≤a$≤\sqrt{3}$.
在平面直角坐标系的第一象限内,边长为1的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a),如图,双曲线y=$\frac{3}{x}$(x>0)与此正方形的边有交点,则a的取值范围是$\sqrt{3}$-1≤a$≤\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
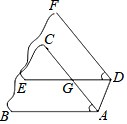 如图,某同学剪了两片角度均为50°的硬板纸纸片(∠BAC=∠EDF=50°),将其中一片平移,连结AD,如果△AGD中有两个角相等,则∠GAD的度数为50°或80°或65°.
如图,某同学剪了两片角度均为50°的硬板纸纸片(∠BAC=∠EDF=50°),将其中一片平移,连结AD,如果△AGD中有两个角相等,则∠GAD的度数为50°或80°或65°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
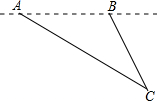 活动一:如图,飞机在距地面9km高空上飞行,先在A处测得正前方某小岛C的俯角为30°,飞行一段距离后,在B处测得该小岛的俯角为60°.求飞机的飞行距离.
活动一:如图,飞机在距地面9km高空上飞行,先在A处测得正前方某小岛C的俯角为30°,飞行一段距离后,在B处测得该小岛的俯角为60°.求飞机的飞行距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com