
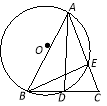
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.
求证:(1)、D是BC的中点;(2)、△BEC∽△ADC;(3)、若![]() ,求⊙O的半径。
,求⊙O的半径。
【答案】(1)、证明过程见解析;(2)证明见解析;(3)、3.
【解析】
试题分析:(1)、根据直径所对的圆周角为直角得出AD为高线,然后根据等腰三角形的三线合一定理进行说明;(2)、根据同弧所对的圆周角相等得出∠CBE=∠CAD,然后根据∠BCE=∠ACD说明三角形相似;(3)、根据三角形相似进行求解.
![]() 试题解析:(1)、∵AB是⊙O的直径, ∴∠ADB=90° 即AD是底边BC上的高.
试题解析:(1)、∵AB是⊙O的直径, ∴∠ADB=90° 即AD是底边BC上的高.
又∵AB=AC,∴△ABC是等腰三角形, ∴D是BC的中点
(2)、∵∠CBE与∠CAD是同弧所对的圆周角,∴ ∠CBE=∠CAD.
又∵ ∠BCE=∠ACD, ∴△BEC∽△ADC;
(3)、由△BEC∽△ADC得:![]() , 即CD·BC=AC·CE. ∵D是BC的中点,∴CD=
, 即CD·BC=AC·CE. ∵D是BC的中点,∴CD=![]() BC.
BC.
又 ∵AB=AC,∴CD·BC=AC·CE=![]() BC ·BC=AB·CE 即BC
BC ·BC=AB·CE 即BC![]() =2AB·CE=12
=2AB·CE=12
∴AB=6 ∴⊙O的半径为3……12分


科目:初中数学 来源: 题型:
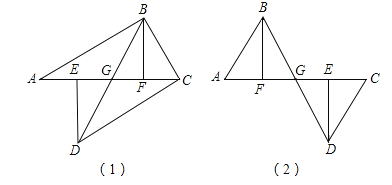
【题目】如图(1),A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,BF⊥AC,若AB=CD,试证明BD平分EF,若将△DEC的边EC沿AC方向移动变为图(2)时,其余条件不变,上述结论是否成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点P(﹣2,3)关于x轴对称的点的坐标为( )
A. (﹣2,﹣3) B. (2,﹣3) C. (﹣3,﹣2) D. (3,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列命题:
(1)三角形的一个外角一定大于它的一个内角
(2)若一个三角形的三个内角之比为1:3:4,它肯定是直角三角形
(3)一个多边形的内角和是540°,则这个多边形是五边形
(4)在同一平面内,平行于同一条直线的两条直线平行
(5)在同一平面内,过一点有且只有一条直线与已知直线垂直
其中真命题的个数是( )
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两站间的路程为450 km,一列慢车从甲站开出,每小时行驶65 km,一列快车从乙站开出,每小时行驶85 km.
(1)两车同时开出相向而行,多少小时相遇?
(2)快车先开1小时两车相向而行,慢车行驶多少小时两车相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com