
【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M,N分别是斜边AB,DE的中点,点P为AD的中点,连接AE、BD、MN.
(1)求证:△PMN为等腰直角三角形;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP,BD分别交于点G、H,请判断①中的结论是否成立,若成立,请证明;若不成立,请说明理由.

【答案】(1)证明见解析;(2)成立,理由见解析.
【解析】
(1)由等腰直角三角形的性质易证△ACE≌△BCD,由此可得AE=BD,再根据三角形中位线定理即可得到PM=PN,由平行线的性质可得PM⊥PN,于是得到结论;
(2)(1)中的结论仍旧成立,由(1)中的证明思路即可证明.
(1)∵△ACB和△ECD是等腰直角三角形,
∴AC=BC,EC=CD,∠ACB=∠ECD=90°.
在△ACE和△BCD中,
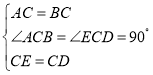 ,
,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠EAC=∠CBD,
∵∠CBD+∠BDC=90°,
∴∠EAC+∠BDC=90°,
∵点M、N分别是斜边AB、DE的中点,点P为AD的中点,
∴PM=![]() BD,PN=
BD,PN=![]() AE,
AE,
∴PM=PN,
∵PM∥BD,PN∥AE,
∴∠NPD=∠EAC,∠MPA=∠BDC,
∵∠EAC+∠BDC=90°,
∴∠MPA+∠NPC=90°,
∴∠MPN=90°,
即PM⊥PN,
∴△PMN为等腰直角三角形;
(2)①中的结论成立,
理由:设AE与BC交于点O,如图②所示:
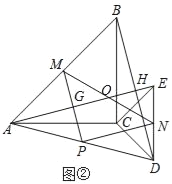
∵△ACB和△ECD是等腰直角三角形,
∴AC=BC,EC=CD,∠ACB=∠ECD=90°.
∴∠ACE=∠BCD,
在△ACE和△BCD中,
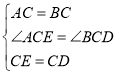 ,
,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠CAE=∠CBD.
∵∠AOC=∠BOE,∠CAE=∠CBD,
∴∠BHO=∠ACO=90°,
∴AE⊥BD,
∵点P、M、N分别为AD、AB、DE的中点,
∴PM=![]() BD,PM∥BD,PN=
BD,PM∥BD,PN=![]() AE,PN∥AE,
AE,PN∥AE,
∴PM=PN.
∵AE⊥BD,
∴PM⊥PN,
∴△PMN为等腰直角三角形.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】乔亚萍做一道数学题,“已知两个多项式![]()
![]() ,
,![]() ,试求
,试求![]() .”其中多项式
.”其中多项式![]() 的二次项系数印刷不清楚
的二次项系数印刷不清楚
(1)乔亚萍看了答案以后知道![]() ,请你替乔亚萍求出多项式
,请你替乔亚萍求出多项式![]() 的二次项系数;
的二次项系数;
(2)在(1)的基础上,乔亚萍已经将多项式![]() 正确求出,老师又给出了一个多项式
正确求出,老师又给出了一个多项式![]() ,要求乔亚萍求出
,要求乔亚萍求出![]() 的结果.乔亚萍在求解时,误把“
的结果.乔亚萍在求解时,误把“![]() ”看成“
”看成“![]() ”,结果求出的答案为
”,结果求出的答案为![]() ,请你替乔亚萍求出“
,请你替乔亚萍求出“![]() ”的正确答案.
”的正确答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,随着我国科学技术的迅猛发展,很多行业已经由“中国制造”升级为“中国创造”,高铁事业是“中国创造”的典范,甲、乙两个城市的火车站相距1280千米,加开高铁后,从甲站到乙站的运行时间缩短了11个小时,大大方便了人们出行,已知高铁行驶速度是原来火车速度的3.2倍,求高铁的行驶速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
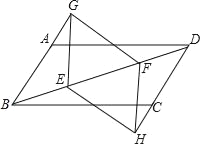
【题目】如图,在ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.
求证:(1)△BEG≌△DFH;
(2)四边形GEHF是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,AC=BC,∠A=30°,点D在AB边上,且∠ADC=45°.
(1)求∠BCD的度数;
(2)将图1中的△BCD绕点B顺时针旋转得到△BC′D′,当点D′恰好落在BC边上时,如图2所示,连接C′C并延长交AB于点E.
①求∠C′CB的度数;
②求证:△C′BD′≌△CAE.
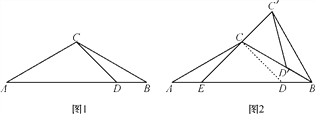
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.
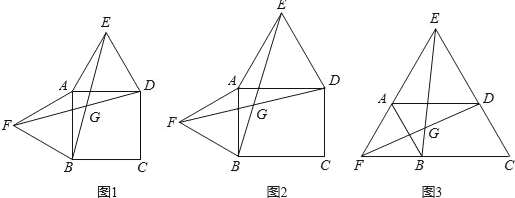
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导“节约用水,从我做起”,鼓楼区政府决定对区直属机关300户家庭的用水情况作一次调查,区政府调查小组随机抽查了其中某些家庭一年的月平均用水量(单位:吨),调查中发现,每户用水量每月均在10﹣14吨范围,并将调查结果制成了如图所示的条形统计图(不完整)和扇形统计图.
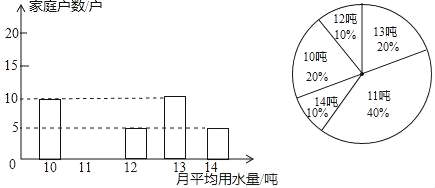
(1)请将条形统计图补充完整;
(2)这些家庭月用水量数据的平均数是 ,众数是 ,中位数是 ;
(3)根据样本数据,估计鼓楼区直属机关300户家庭中月平均用水量不超过12吨的约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于受到手机更新换代的影响,某店经销的甲型号手机今年的售价比去年每台降价500元.如果卖出相同数量的手机,那么去年销售额为8万元,今年销售额只有6万元.
(1)今年甲型号手机每台售价为多少元?
(2)为了提高利润,该店计划购进乙型号手机销售,已知甲型号手机每台进价为1000元,乙型号手机每台进价为800元,预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20台,请问有几种进货方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com