
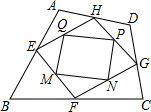
 如图,在四边形ABCD中,依次将其各边的中点E、F、G、H连接起来,得到的四边形EFGH是平行四边形,再依次将四边形EFGH各边的中点M、N、P、Q连接起来,得到的四边形MNPQ.
如图,在四边形ABCD中,依次将其各边的中点E、F、G、H连接起来,得到的四边形EFGH是平行四边形,再依次将四边形EFGH各边的中点M、N、P、Q连接起来,得到的四边形MNPQ.分析 (1)连接EG,根据三角形的中位线的性质得到QP∥EG,QP=$\frac{1}{2}$EG,MN∥EG,MN=$\frac{1}{2}$EG,于是得到QP∥MN,QP=MN,即可得到四边形MNPQ是平行四边形;
(2)根据题意写出命题即可.
解答 解:(1)四边形MNPQ是平行四边形;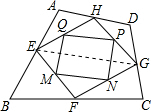 证明:连接EG,
证明:连接EG,
∵点M、N、P、Q分别是四边形EFGH各边的中点,
∴QP∥EG,QP=$\frac{1}{2}$EG,MN∥EG,MN=$\frac{1}{2}$EG,
∴QP∥MN,QP=MN,
∴四边形MNPQ是平行四边形;
(2)已知:在四边形ABCD中,AC⊥BD,点E、F、G、H分别是四边形ABCD四边的中点,依次将其各边的中点E、F、G、H连接起来,得到的四边形EFGH是平行四边形,再依次将四边形EFGH各边的中点M、N、P、Q连接起来,得到的四边形MNPQ,
求证:四边形MNPQ是菱形.
点评 本题考查了中点四边形,平行四边形的判定,命题,三角形的中位线,熟练掌握三角形的中位线是解题的关键.


科目:初中数学 来源: 题型:解答题
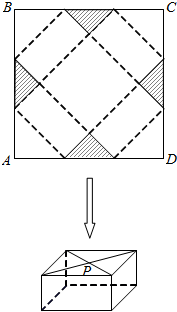 如图,四边形ABCD是边长为60cm的正方形硬纸片,剪掉阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使A、B、C、D四个点重合于图中的点P,正好形成一个底面是正方形的长方体包装盒.
如图,四边形ABCD是边长为60cm的正方形硬纸片,剪掉阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使A、B、C、D四个点重合于图中的点P,正好形成一个底面是正方形的长方体包装盒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
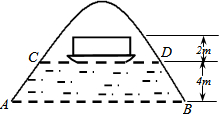 去年2月份下旬的某双休日赵化中学组织教职工以及家属游兴文石林时,有几个数学老师发现有一个地下河的进口处是一呈抛物线状的天然拱洞,未涨水时测得水面宽AB是10米,当涨水水面上升4米后,测得水面宽CD为6米.
去年2月份下旬的某双休日赵化中学组织教职工以及家属游兴文石林时,有几个数学老师发现有一个地下河的进口处是一呈抛物线状的天然拱洞,未涨水时测得水面宽AB是10米,当涨水水面上升4米后,测得水面宽CD为6米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 两个城镇A,B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路,现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A,B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.
两个城镇A,B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路,现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A,B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{72}{x+2}$=$\frac{72}{x}$+3 | B. | $\frac{72}{x-2}$=$\frac{72}{x}$-3 | C. | $\frac{72}{x-2}$=$\frac{72}{x}$+3 | D. | $\frac{72}{x+2}$=$\frac{72}{x}$-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 赚了$\frac{1}{6}$a元 | B. | 赔了$\frac{1}{6}$a元 | C. | 赚了$\frac{1}{12}$a元 | D. | 不赚不赔 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com