
【题目】如图,△ABC中,AP垂直∠ABC的平分线BP于点P.若△ABC的面积为32cm2,BP=6cm,且△APB的面积是△APC的面积的3倍.则AP=________cm.

【答案】4
【解析】延长AP交BC于E,根据AP垂直∠B的平分线BP于P,即可求出△ABP≌△EBP,又知△APC和△CPE等底同高,可以证明两三角形面积相等,再根据已知条件△ABC的面积为32cm2,即可求得△APB的面积,再根据面积公式即可求得AP的长.
如图所示:延长AP交BC于E,
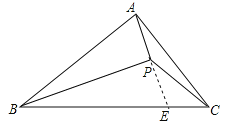
∵AP垂直∠B的平分线BP于P,
∴∠ABP=∠EBP,∠APB=∠BPE=90°,
在△ABP和△EBP中,

∴△ABP≌△EBP(ASA),
∴S△ABP=S△EBP,AP=EP,
∴△APC和△CPE等底同高,
∴S△APC=S△PCE,
∵S△ABP=3S△APC,
∴S△EBP=3S△PCE,
设S△PCE=x,则S△APC=x, S△ABP=S△EBP=3x,
∵△ABC的面积为32cm2
∴x+x+3x+3x=32,
∴x=4,
∴S△ABP=13.
∵AP垂直∠ABC的平分线BP于点P,
∴S△ABP=![]() =12
=12
又∵BP=6cm
∴AP=4


科目:初中数学 来源: 题型:
【题目】某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植﹣亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
(1)在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(2)分别求出政府补贴政策实施后,种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式;
(3)要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?并求出总收益w的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生到距离学校6千米的科技馆去参观,小华因事没能乘上学校的包车,于是准备在学校门口改乘出租车去科技馆,出租车收费标准有两种类型,如下表:
里程 | 甲类收费(元) | 乙类收费(元) |
3千米以下(包含3千米) | 7.00 | 6.00 |
3千米以上,每增加1千米 | 1.60 | 1.40 |
(1)设出租车行驶的里程为x千米(![]() 且x取正整数),分别写出两种类型的总收费(用含x的代数式表示);
且x取正整数),分别写出两种类型的总收费(用含x的代数式表示);
(2)小华身上仅有11元,他乘出租车到科技馆车费够不够请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD于点Q,连接CQ。取CQ的中点M,连接MD,MP,若MD⊥MP,则AQ的长________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品用了160元.
(1)求A,B两种商品每件各是多少元?
(2)如果小亮准备购买A,B两种商品共10件,总费用不超过350元,但不低于300元,问有几种购买方案,哪种方案费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形OABC的顶点O在原点。
(1)如图①,点C的坐标为(![]() ,
,![]() ),且实数
),且实数![]() ,
,![]() 满足
满足![]() ,求C点的坐标及线段0C的长度;
,求C点的坐标及线段0C的长度;
(2)如图②,点F在BC上,AB交x轴于点E,EF,OC的延长线交于点G,EG=OG,求∠EOF的度数;
(3)如图③,将(1)中正方形OABC绕点O顺时针旋转,使OA落在y轴上,E为AB上任意一点,OE的垂直平分线交x轴于点G,交OE于点P,连接EG交BC于点F,求△BEF的周长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AEF=80°,且∠A=x°,∠C=y°,∠F=z°.若![]() +|y-80-m|+|z-40|=0(m为常数,且0<m<100)
+|y-80-m|+|z-40|=0(m为常数,且0<m<100)
(1) 求∠A、∠C的度数(用含m的代数式表示)
(2) 求证:AB∥CD
(3) 若∠A=40°,∠BAM=20°,∠EFM=10°,直线AM与直线FM交于点M,直接写出∠AMF的度数


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com