
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½ČĖ¼Ó¹¤Ķ¬Ņ»ÖÖĮć¼ž£¬¼×ĆæĢģ¼Ó¹¤µÄŹżĮæŹĒŅŅĆæĢģ¼Ó¹¤ŹżĮæµÄ1.5±¶£¬Į½ČĖø÷¼Ó¹¤300øöÕāÖÖĮć¼ž£¬¼×±ČŅŅÉŁÓĆ5Ģģ£®
£Ø1£©Ēó¼×”¢ŅŅĮ½ČĖĆæĢģø÷¼Ó¹¤¶ąÉŁøöÕāÖÖĮć¼ž£æ
£Ø2£©ŅŃÖŖ¼×”¢ŅŅĮ½ČĖ¼Ó¹¤ÕāÖÖĮć¼žĆæĢģµÄ¼Ó¹¤·Ń·Ö±šŹĒ150ŌŖŗĶ120ŌŖ£¬ĻÖÓŠ1500øöÕāÖÖĮć¼žµÄ¼Ó¹¤ČĪĪń£¬¼×µ„¶Ą¼Ó¹¤Ņ»¶ĪŹ±¼äŗóĮķÓŠ°²ÅÅ£¬Ź£ÓąČĪĪńÓÉŅŅµ„¶ĄĶź³É£®Čē¹ū×ܼӹ¤·ŃĪŖ7800ŌŖ£¬ÄĒĆ“¼×”¢ŅŅø÷¼Ó¹¤ĮĖ¶ąÉŁĢģ£æ
”¾“š°ø”æ£Ø1£©¼×ĆæĢģ¼Ó¹¤30øöĮć¼ž£¬ŅŅĆæĢģ¼Ó¹¤20øöĮć¼ž£»£Ø2£©¼×¼Ó¹¤ĮĖ40Ģģ£¬ŅŅ¼Ó¹¤ĮĖ15Ģģ£®
”¾½āĪö”æ
£Ø1£©ÉčŅŅĆæĢģ¼Ó¹¤xøöĮć¼ž£¬Ōņ¼×ĆæĢģ¼Ó¹¤1.5xøöĮć¼ž£¬øł¾Ż¼×±ČŅŅÉŁÓĆ5Ģģ£¬ĮŠ·ÖŹ½·½³ĢĒó½ā£»
£Ø2£©Éč¼×¼Ó¹¤ĮĖaĢģ£¬ŅŅ¼Ó¹¤ĮĖbĢģ£¬øł¾Ż1500øöĮć¼ž£¬ĮŠ·½³Ģ£»øł¾Ż×ܼӹ¤·ŃĪŖ7800ŌŖ£¬ĮŠ·½³Ģ£¬½ā³öa£¬b¼“æÉ£®
½ā£ŗ£Ø1£©ÉčŅŅĆæĢģ¼Ó¹¤xøöĮć¼ž£¬Ōņ¼×ĆæĢģ¼Ó¹¤1.5xøöĮć¼ž£¬ÓÉĢāŅāµĆ£ŗ
![]()
Č„·ÖÄøµĆ£ŗ300”Į1.5£½300£«5”Į1.5x
½āµĆx£½20
¾¼ģŃ飬x£½20ŹĒ·ÖŹ½·½³ĢµÄ½āĒŅ·ūŗĻŹµ¼ŹŅāŅ壮
”ą1.5x£½30
“š£ŗ¼×ĆæĢģ¼Ó¹¤30øöĮć¼ž£¬ŅŅĆæĢģ¼Ó¹¤20øöĮć¼ž£®
£Ø2£©Éč¼×¼Ó¹¤ĮĖaĢģ£¬ŅŅ¼Ó¹¤ĮĖbĢģ£¬ŌņÓÉĢāŅāµĆ![]()
½āµĆ£ŗa=40£¬b=15£¬
µ±a£½40Ź±£¬b£½15£¬·ūŗĻĪŹĢāµÄŹµ¼ŹŅāŅ壮
“š£ŗ¼×¼Ó¹¤ĮĖ40Ģģ£¬ŅŅ¼Ó¹¤ĮĖ15Ģģ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬¾ŲŠĪABCDµÄŅ»±ßBCŌŚÖ±½Ē×ų±źĻµÖŠxÖįÉĻ£¬ÕŪµž±ßAD£¬Ź¹µćDĀäŌŚxÖįÉĻµćF“¦£¬ÕŪŗŪĪŖAE£¬ŅŃÖŖAB£½8£¬AD£½10£¬²¢ÉčµćB×ų±źĪŖ£Øm£¬0£©£¬ĘäÖŠm£¼0£®
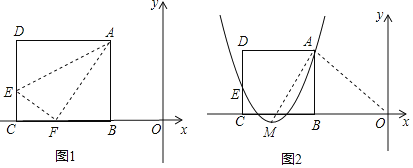
£Ø1£©ĒóµćE”¢FµÄ×ų±ź£ØÓĆŗ¬mµÄŹ½×Ó±ķŹ¾£©£»
£Ø2£©Į¬½ÓOA£¬Čō”÷OAFŹĒµČŃüČż½ĒŠĪ£¬ĒómµÄÖµ£»
£Ø3£©ČēĶ¼2£¬ÉčÅ×ĪļĻßy£½a£Øx©m+6£©2+h¾¹żA”¢EĮ½µć£¬Ę䶄µćĪŖM£¬Į¬½ÓAM£¬Čō”ĻOAM£½90”ć£¬Ēóa”¢h”¢mµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬ŌŚĶ¬Ņ»Ö±½Ē×ų±źĻµxOyÖŠ£¬ÓŠĖ«ĒśĻß![]() £¬Ö±Ļßy2£½k2x+b1£¬y3£½k3x+b2£¬ĒŅµćA(2£¬5)£¬µćB(©6£¬n)ŌŚĖ«ĒśĻßµÄĶ¼ĻóÉĻ
£¬Ö±Ļßy2£½k2x+b1£¬y3£½k3x+b2£¬ĒŅµćA(2£¬5)£¬µćB(©6£¬n)ŌŚĖ«ĒśĻßµÄĶ¼ĻóÉĻ
£Ø1£©Ēóy1ŗĶy2µÄ½āĪöŹ½£»
£Ø2£©Čōy3ÓėÖ±Ļßx£½4½»ÓŚĖ«ĒśĻߣ¬ĒŅy3”Īy2£¬Ēóy3µÄ½āĪöŹ½£»
£Ø3£©Ö±½ÓŠ“³ö![]() µÄ½ā¼Æ£®
µÄ½ā¼Æ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻß![]()
![]() ¾¹ż
¾¹ż![]() £¬
£¬![]() Į½µć£¬µć
Į½µć£¬µć![]() ĪŖÅ×ĪļĻߵĶ„µć£¬Å×ĪļĻߵĶŌ³ĘÖįÓė
ĪŖÅ×ĪļĻߵĶ„µć£¬Å×ĪļĻߵĶŌ³ĘÖįÓė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() £®
£®

£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©¶Æµć![]() “Óµć
“Óµć![]() ³ö·¢£¬ŃŲĻ߶Ī
³ö·¢£¬ŃŲĻ߶Ī![]() ĻņÖÕµć
ĻņÖÕµć![]() ×÷ŌČĖŁŌĖ¶Æ£¬ĖŁ¶ČĪŖĆæĆė1øöµ„Ī»³¤¶Č£¬ŌĖ¶ÆŹ±¼äĪŖ
×÷ŌČĖŁŌĖ¶Æ£¬ĖŁ¶ČĪŖĆæĆė1øöµ„Ī»³¤¶Č£¬ŌĖ¶ÆŹ±¼äĪŖ![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() £¬½»
£¬½»![]() ÓŚµć
ÓŚµć![]() £¬ŅŌ
£¬ŅŌ![]() ĪŖÕż·½ŠĪµÄŅ»±ß£¬ĻņÉĻ×÷Õż·½ŠĪ
ĪŖÕż·½ŠĪµÄŅ»±ß£¬ĻņÉĻ×÷Õż·½ŠĪ![]() £¬±ß
£¬±ß![]() ½»
½»![]() ÓŚµć
ÓŚµć![]() £¬ŃÓ³¤
£¬ŃÓ³¤![]() ½»
½»![]() ÓŚµć
ÓŚµć![]() £®
£®
¢Łµ±![]() ĪŖŗĪÖµŹ±£¬µć
ĪŖŗĪÖµŹ±£¬µć![]() ĀäŌŚÅ×ĪļĻßÉĻ£»
ĀäŌŚÅ×ĪļĻßÉĻ£»
¢ŚŌŚµć![]() ŌĖ¶Æ¹ż³ĢÖŠ£¬ŹĒ·ń“ęŌŚÄ³Ņ»Ź±æĢ£¬Ź¹µĆĖıߊĪ
ŌĖ¶Æ¹ż³ĢÖŠ£¬ŹĒ·ń“ęŌŚÄ³Ņ»Ź±æĢ£¬Ź¹µĆĖıߊĪ![]() ĪŖĘ½ŠŠĖıߊĪ£æČō“ęŌŚ£¬Ēó³ö“ĖŹ±æĢµÄ
ĪŖĘ½ŠŠĖıߊĪ£æČō“ęŌŚ£¬Ēó³ö“ĖŹ±æĢµÄ![]() Öµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
Öµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻß![]() Óė
Óė![]() ÖįĻą½»ÓŚ
ÖįĻą½»ÓŚ![]() ”¢
”¢![]() Į½µć£¬Óė
Į½µć£¬Óė![]() ÖįĻą½»ÓŚµć
ÖįĻą½»ÓŚµć![]() £¬ĒŅµć
£¬ĒŅµć![]() Óėµć
Óėµć![]() µÄ×ų±ź·Ö±šĪŖ
µÄ×ų±ź·Ö±šĪŖ![]() £¬
£¬![]() £¬µć
£¬µć![]() ŹĒÅ×ĪļĻߵĶ„µć£®
ŹĒÅ×ĪļĻߵĶ„µć£®

£Ø1£©Ē󶞓ĪŗÆŹżµÄ¹ŲĻµŹ½£®
£Ø2£©µć![]() ĪŖĻ߶Ī
ĪŖĻ߶Ī![]() ÉĻŅ»øö¶Æµć£¬¹żµć
ÉĻŅ»øö¶Æµć£¬¹żµć![]() ×÷
×÷![]() ÖįÓŚµć
ÖįÓŚµć![]() £®Čō
£®Čō![]() £¬
£¬![]() µÄĆ껿ĪŖ
µÄĆ껿ĪŖ![]() £®
£®
¢ŁĒó![]() Óė
Óė![]() µÄŗÆŹż¹ŲĻµŹ½£¬Š“³ö×Ō±äĮæ
µÄŗÆŹż¹ŲĻµŹ½£¬Š“³ö×Ō±äĮæ![]() µÄȔֵ·¶Ī§£®
µÄȔֵ·¶Ī§£®
¢Śµ±![]() Č”µĆ×īÖµŹ±£¬Ēóµć
Č”µĆ×īÖµŹ±£¬Ēóµć![]() µÄ×ų±ź£®
µÄ×ų±ź£®
£Ø3£©ŌŚ![]() ÉĻŹĒ·ń“ęŌŚµć
ÉĻŹĒ·ń“ęŌŚµć![]() £¬Ź¹
£¬Ź¹![]() ĪŖÖ±½ĒČż½ĒŠĪ£æČē¹ū“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµć
ĪŖÖ±½ĒČż½ĒŠĪ£æČē¹ū“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµć![]() µÄ×ų±ź£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄ×ų±ź£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
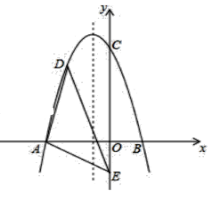
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬¶ž“ĪŗÆŹży£½ax2£«bx£«c½»xÖįÓŚA(£4,0)”¢B(2,0)£¬ŌŚyÖįÉĻÓŠŅ»µć E(0£¬£2)£¬Į¬½ÓAE£®
 ””””””””
””””””””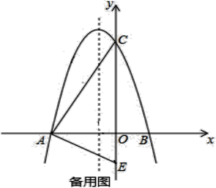
£Ø1£©Ē󶞓ĪŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©µćDŹĒµŚ¶žĻóĻŽÄŚµÄÅ×ĪļĻßÉĻŅ»¶Æµć£®Čōtan”ĻAED£½![]() £¬Ēó“ĖŹ±µćD×ų±ź£»
£¬Ēó“ĖŹ±µćD×ų±ź£»
£Ø3£©Į¬½ÓAC£¬µćPŹĒĻ߶ĪCAÉĻµÄ¶Æµć£¬Į¬½ÓOP£¬°ŃĻ߶ĪPOČĘ×ŵćPĖ³Ź±ÕėŠż×Ŗ90”ćÖĮPQ£¬µćQŹĒµćOµÄ¶ŌÓ¦µć£®µ±¶ÆµćP“ÓµćCŌĖ¶Æµ½µćAŹ±£¬ÅŠ¶Ļ¶ÆµćQµÄ¹ģ¼£²¢Ēó¶ÆµćQĖł¾¹żµÄĀ·¾¶³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£¼Ę»®×éÖÆѧɜ²Ī¼Ó”°Źé·Ø”±”¢”°ÉćÓ°”±”¢”°ŗ½Ä£”±”¢”°Ī§Ęå”±ĖÄøöæĪĶāŠĖȤŠ”×飬ŅŖĒóĆæČĖ±ŲŠė²Ī¼Ó£¬²¢ĒŅÖ»ÄÜŃ”ŌńĘäÖŠŅ»øöŠ”×飬ĪŖĮĖ½āѧɜ¶ŌĖÄøöæĪĶāŠĖȤŠ”×éµÄŃ”ŌńĒéæö£¬Ń§Š£“ÓČ«Ģåѧɜ֊Ė껜³éČ”²æ·Öѧɜ½ųŠŠĪŹ¾ķµ÷²é£¬²¢°Ńµ÷²é½į¹ūÖĘ³ÉČēĶ¼ĖłŹ¾µÄÉČŠĪĶ³¼ĘĶ¼ŗĶĢõŠĪĶ³¼ĘĶ¼(²æ·ÖŠÅĻ¢Ī“øų³ö)£¬ĒėÄćøł¾Żøų³öµÄŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ

£Ø1£©Ēó²Ī¼ÓÕā“ĪĪŹ¾ķµ÷²éµÄѧɜČĖŹż£¬²¢²¹Č«ĢõŠĪĶ³¼ĘĶ¼(»Ķ¼ŗóĒė±ź×¢ĻąÓ¦µÄŹż¾Ż)£»
£Ø2£©m£½_______£¬n£½_______£»
£Ø3£©ČōøĆŠ£¹²ÓŠ1200Ćūѧɜ£¬ŹŌ¹Ą¼ĘøĆŠ£Ń”Ōń”°Ī§Ęå”±æĪĶāŠĖȤŠ”×éµÄѧɜӊ¶ąÉŁČĖ£æ
£Ø4£©·Ö±šÓĆA”¢B”¢C”¢D±ķŹ¾”°Źé·Ø”±”¢”°ÉćÓ°”±”¢”°ŗ½Ä£”±”¢”°Ī§Ęå”±£¬Š”Ć÷ŗĶŠ”ŗģ“ÓÖŠø÷єȔŅ»øöŠ”×飬ĒėÓĆŹ÷דĶ¼·Ø»ņĮŠ±ķ·ØĒó³ö”°Į½ČĖŃ”ŌńŠ”×é²»Ķ¬”±µÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÅ×ĪļĻß![]() ÓėÖ±Ļß
ÓėÖ±Ļß![]() ½»ÓŚµć
½»ÓŚµć![]() £¬µć
£¬µć![]() £®
£®
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©µć![]() ŹĒ
ŹĒ![]() ÖįÉĻ·½Å×ĪļĻßÉĻŅ»µć£¬µć
ÖįÉĻ·½Å×ĪļĻßÉĻŅ»µć£¬µć![]() ŹĒÖ±Ļß
ŹĒÖ±Ļß![]() ÉĻŅ»µć£¬Čō
ÉĻŅ»µć£¬Čō![]() ŅŌĪŖ¶„µćµÄĖıߊĪŹĒŅŌ
ŅŌĪŖ¶„µćµÄĖıߊĪŹĒŅŌ ![]() ĪŖ±ßµÄĘ½ŠŠĖıߊĪ£¬Ēóµć
ĪŖ±ßµÄĘ½ŠŠĖıߊĪ£¬Ēóµć![]() µÄ×ų±ź£®
µÄ×ų±ź£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
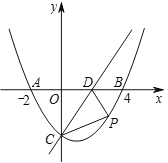
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻß![]() Óė
Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() £¬
£¬![]() £¬ÓėÖ±Ļß
£¬ÓėÖ±Ļß![]() ½»ÓŚµć
½»ÓŚµć![]() £¬Ö±Ļß
£¬Ö±Ļß![]() Óė
Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() £®
£®
(1)ĒóøĆÅ×ĪļĻߵĽāĪöŹ½£®
(2)µć![]() ŹĒÅ×ĪļĻßÉĻµŚĖÄĻóĻŽÉĻµÄŅ»øö¶Æµć£¬Į¬½Ó
ŹĒÅ×ĪļĻßÉĻµŚĖÄĻóĻŽÉĻµÄŅ»øö¶Æµć£¬Į¬½Ó![]() £¬
£¬![]() £¬µ±
£¬µ±![]() µÄĆ껿×ī“óŹ±£¬Ēóµć
µÄĆ껿×ī“óŹ±£¬Ēóµć![]() µÄ×ų±ź£®
µÄ×ų±ź£®
(3)½«Å×ĪļĻߵĶŌ³ĘÖįĻņ×óĘ½ŅĘ3øö³¤¶Čµ„Ī»µĆµ½Ö±Ļß![]() £¬µć
£¬µć![]() ŹĒÖ±Ļß
ŹĒÖ±Ļß![]() ÉĻŅ»µć£¬Į¬½Ó
ÉĻŅ»µć£¬Į¬½Ó![]() £¬
£¬![]() £¬ČōÖ±Ļß
£¬ČōÖ±Ļß![]() ÉĻ“ęŌŚŹ¹
ÉĻ“ęŌŚŹ¹![]() ×ī“óµÄµć
×ī“óµÄµć![]() £¬ĒėÖ±½ÓŠ“³öĀś×ćĢõ¼žµÄµć
£¬ĒėÖ±½ÓŠ“³öĀś×ćĢõ¼žµÄµć![]() µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com