
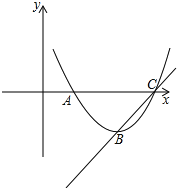
【题目】已知抛物线y1=ax2+bx+c(a≠0,a≠c)过点A(1,0),顶点为B,且抛物线不经过第三象限.
(1)使用a、c表示b;
(2)判断点B所在象限,并说明理由;
(3)若直线y2=2x+m经过点B,且交抛物线于另一点C(![]() ,b+8),求当x≥1时,y1的取值范围.
,b+8),求当x≥1时,y1的取值范围.
【答案】(1)b=-a-c;(2)第四象限,理由见解析;(3)y1≥-2.
【解析】
试题分析:此题主要考查了二次函数的综合应用以及根与系数的关系和一次函数与二次函数交点问题等知识,根据数形结合得出是解题关键.
(1)抛物线经过A(1,0),把点代入函数即可得到b=-a-c;
(2)判断点在哪个象限,需要根据题意画图,由条件:图象不经过第三象限就可以推出开口向上,a>0,只需要知道抛物线与x轴有几个交点即可解决,判断与x轴有两个交点,一个可以考虑△,由△就可以判断出与x轴有两个交点,所以在第四象限;或者直接用公式法(或十字相乘法)算出,由两个不同的解x1=1,x2=![]() ,(a≠c),进而得出点B所在象限;
,(a≠c),进而得出点B所在象限;
(3)当x≥1时,y1的取值范围,只要把图象画出来就清晰了,难点在于要观察出C(![]() ,b+8)是抛物线与x轴的另一个交点,理由是x1=1,x2=
,b+8)是抛物线与x轴的另一个交点,理由是x1=1,x2=![]() ,(a≠c),由这里可以发现,b+8=0,b=-8,a+c=8,还可以发现C在A的右侧;可以确定直线经过B、C两点,看图象可以得到,x≥1时,y1大于等于最小值,此时算出二次函数最小值即可,即求出
,(a≠c),由这里可以发现,b+8=0,b=-8,a+c=8,还可以发现C在A的右侧;可以确定直线经过B、C两点,看图象可以得到,x≥1时,y1大于等于最小值,此时算出二次函数最小值即可,即求出![]() 即可,已经知道b=-8,a+c=8,算出a,c即可,即可得出y1的取值范围.
即可,已经知道b=-8,a+c=8,算出a,c即可,即可得出y1的取值范围.
试题解析:(1)∵抛物线y1=ax2+bx+c(a≠0,a≠c),经过A(1,0),
把点代入函数即可得到:b=-a-c;
(2)B在第四象限.
理由如下:
∵抛物线y1=ax2+bx+c(a≠0,a≠c)过点A(1,0),
∴x1=1,x2=![]() ,a≠c,
,a≠c,
所以抛物线与x轴有两个交点,
又因为抛物线不经过第三象限,
所以a>0,且顶点在第四象限;
(3)∵C(![]() ,b+8),且在抛物线上,
,b+8),且在抛物线上,
∴b+8=0,∴b=-8,
∵a+c=-b,
∴a+c=8,
把B、C两点代入直线解析式易得:c-a=4,
即![]() ,
,
解得:![]() ,
,
如图所示,C在A的右侧,
∴当x≥1时,y1≥![]() =-2.
=-2.


科目:初中数学 来源: 题型:
【题目】据报道2018年4月,某市土地出让金达11.9亿,比2017年同期的7.984亿上涨幅度达到48.8%,其中数值11.9亿可用科学记数法表示为( )
A. 1.19×109 B. 11.9×108 C. 1.19×1010 D. 11.9×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜经营户从蔬菜批发市场批发蔬菜进行零售,部分蔬菜批发价格与零售价格如表:
蔬菜品种 | 西红柿 | 青椒 | 西兰花 | 豆角 |
批发价(元/㎏) | 3.6 | 5.4 | 8 | 4.8 |
零售价(元/㎏) | 5.4 | 8.4 | 14 | 7.6 |
请解答下列问题:
(1)第一天,该经营户批发西红柿和西兰花两种蔬菜共300㎏,用去了1520元钱,这两种蔬菜当天全部售完一共赚了多少元钱?
(2)第二天,该经营户用1520元仍然批发西红柿和西兰花,要想当天全部售完后所赚钱数不少于1050元,则该经营户最多能批发西红柿多少㎏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从下列不等式中选择一个与x+1≥2组成不等式组,若要使该不等式组的解集为x≥1,则可以选择的不等式是( )
A. x<2 B. x>2 C. x<0 D. x>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若某次数学考试标准成绩定为85分,规定高于标准记为正,两位学生的成绩分别记作:+9分和-3分,则第一位学生的实际得分为___________分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
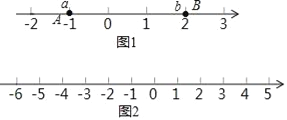
如图1,在数轴上A点衰示的数为a,B点表示的数为b,则点A到点B的距离记为AB.线段AB的长可以用右边的数减去左边的数表示,即AB﹣b﹣a.
请用上面的知识解答下面的问题:
如图2,一个点从数轴上的原点开始,先向左移动1cm到达A点,再向左移动2cm到达B点,然后向右移动7cm到达C点,用1个单位长度表示1cm.
(1)请你在数轴上表示出A.B.C三点的位置:
(2)点C到点人的距离CA= cm;若数轴上有一点D,且AD=4,则点D表示的数为 ;
(3)若将点A向右移动xcm,则移动后的点表示的数为 ;(用代数式表示)
(4)若点B以每秒2cm的速度向左移动,同时A.C点分别以每秒1cm、4cm的速度向右移动.设移动时间为t秒,
试探索:CA﹣AB的值是否会随着t的变化而改变?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
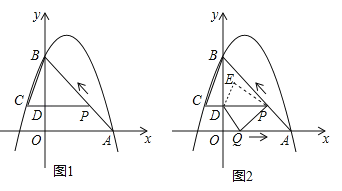
【题目】如图 1,二次函数![]() 的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接 BC ,当t=![]() 时,求△BCP的面积;
时,求△BCP的面积;
(3)如图 2,动点 P 从 A 出发时,动点 Q 同时从 O 出发,在线段 OA 上沿 O→A 的方向以 1个单位长度的速度运动,当点 P 与 B 重合时,P 、 Q 两点同时停止运动,连接 DQ 、 PQ ,将△DPQ沿直线 PC 折叠到 △DPE .在运动过程中,设 △DPE 和 △OAB重合部分的面积为 S ,直接写出 S 与 t 的函数关系式及 t 的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com