
 如图,在△ABC中,点D是BC边的中点,分别过点B、C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:DE=DF.
如图,在△ABC中,点D是BC边的中点,分别过点B、C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:DE=DF.  心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BE平分∠ABC交CD、AC分别于G、E,GF∥AC交AB于F,猜想:EF与AB有怎样的位置关系,请说明理由.
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BE平分∠ABC交CD、AC分别于G、E,GF∥AC交AB于F,猜想:EF与AB有怎样的位置关系,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠ACB=90°,BC=$\sqrt{5}$,AC=2$\sqrt{5}$,
如图,△ABC中,∠ACB=90°,BC=$\sqrt{5}$,AC=2$\sqrt{5}$,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某单位为增强职工的安全意识,举办了安全应急知识竞赛活动,为了解情况,从中抽取部分职工的竞赛成绩(分数为正整数)进行统计,整理成下面的表格和统计图
某单位为增强职工的安全意识,举办了安全应急知识竞赛活动,为了解情况,从中抽取部分职工的竞赛成绩(分数为正整数)进行统计,整理成下面的表格和统计图| 成绩(分) | 49.5-59.5 | 59.5-69.5 | 69.5-79.5 | 79.5-89.5 | 89.5-100.5 |
| 频数(人) | 20 | 32 | a | b | c |
| 频率 | 0.08 | 0.20 | 0.36 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,C为线段AE上一动点(不与点A,E重合),在AE在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤OC平分∠AOE.一定成立的结论有①②③⑤.
如图,C为线段AE上一动点(不与点A,E重合),在AE在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤OC平分∠AOE.一定成立的结论有①②③⑤.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 阴天会下雨是必然事件 | |
| B. | 若关于x的一元二次方程kx2-2x-1=0有实数根,则k≥-1 | |
| C. | 在平面直角坐标系中,如果位似是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k | |
| D. | 多边形的外角和等于360° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
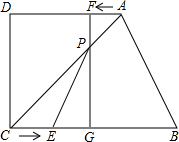 如图,在四边形ABCD中,AD∥BC,∠D=90°,BC=50,AD=36,CD=27.点E从C出发以每秒5个单位长度的速度向B运动,点F从A出发,以每秒4个单位长度的速度向D运动.两点同时出发,当其中一个动点到达终点时,另一个动点也随之停止运动.过点F作FG⊥BC,垂足为G,连结AC交FG于P,连结EP.
如图,在四边形ABCD中,AD∥BC,∠D=90°,BC=50,AD=36,CD=27.点E从C出发以每秒5个单位长度的速度向B运动,点F从A出发,以每秒4个单位长度的速度向D运动.两点同时出发,当其中一个动点到达终点时,另一个动点也随之停止运动.过点F作FG⊥BC,垂足为G,连结AC交FG于P,连结EP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com