
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy=![]() ÓėxÖį½»ÓŚµćA£¬µćB£¬ÓėyÖį½»ÓŚµćC£¬µćDÓėµćC¹ŲÓŚxÖį¶Ō³Ę£¬µćPŹĒxÖįÉĻµÄŅ»øö¶Æµć£¬ÉčµćPµÄ×ų±źĪŖ£Øm£¬0£©£¬¹żµćP×÷xÖįµÄ“¹Ļßl½»Å×ĪļĻßÓŚµćQ£®
ÓėxÖį½»ÓŚµćA£¬µćB£¬ÓėyÖį½»ÓŚµćC£¬µćDÓėµćC¹ŲÓŚxÖį¶Ō³Ę£¬µćPŹĒxÖįÉĻµÄŅ»øö¶Æµć£¬ÉčµćPµÄ×ų±źĪŖ£Øm£¬0£©£¬¹żµćP×÷xÖįµÄ“¹Ļßl½»Å×ĪļĻßÓŚµćQ£®
£Ø1£©ĒóµćA”¢µćB”¢µćCµÄ×ų±ź£»
£Ø2£©ĒóÖ±ĻßBDµÄ½āĪöŹ½£»
£Ø3£©µ±µćPŌŚĻ߶ĪOBÉĻŌĖ¶ÆŹ±£¬Ö±Ļßl½»BDÓŚµćM£¬ŹŌĢ½¾æmĪŖŗĪÖµŹ±£¬ĖıߊĪCQMDŹĒĘ½ŠŠĖıߊĪ£»
£Ø4£©ŌŚµćPµÄŌĖ¶Æ¹ż³ĢÖŠ£¬ŹĒ·ń“ęŌŚµćQ£¬Ź¹”÷BDQŹĒŅŌBDĪŖÖ±½Ē±ßµÄÖ±½ĒČż½ĒŠĪ£æČō“ęŌŚ£¬Ēó³öµćQµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

”¾“š°ø”æ£Ø1£©A£Ø©1£¬0£©£¬B£Ø4£¬0£©£¬C£Ø0£¬2£©£»£Ø2£©![]() £»£Ø3£©m=2£»£Ø4£©QµÄ×ų±źĪŖ£Ø3£¬2£©£¬£Ø8£¬©18£©£¬£Ø©1£¬0£©£®
£»£Ø3£©m=2£»£Ø4£©QµÄ×ų±źĪŖ£Ø3£¬2£©£¬£Ø8£¬©18£©£¬£Ø©1£¬0£©£®
”¾½āĪö”æ
ŹŌĢā£Ø1£©øł¾ŻŗÆŹż½āĪöŹ½ĮŠ·½³Ģ¼“æɵƵ½½įĀŪ£»
£Ø2£©ÓɵćCÓėµćD¹ŲÓŚxÖį¶Ō³Ę£¬µĆµ½D£Ø0£¬©2£©£¬½ā·½³Ģ¼“æɵƵ½½įĀŪ£»
£Ø3£©ČēĶ¼1ĖłŹ¾£ŗøł¾ŻĘ½ŠŠĖıߊĪµÄŠŌÖŹµĆµ½QM=CD£¬ÉčµćQµÄ×ų±źĪŖ£Øm£¬![]() £©£¬ŌņM£Øm£¬
£©£¬ŌņM£Øm£¬![]() £©£¬ĮŠ·½³Ģ¼“æɵƵ½½įĀŪ£»
£©£¬ĮŠ·½³Ģ¼“æɵƵ½½įĀŪ£»
£Ø4£©ÉčµćQµÄ×ų±źĪŖ£Øm£¬![]() £©£¬·ÖĮ½ÖÖĒéæö£ŗ¢Łµ±”ĻQBD=90”揱£¬øł¾Ż¹“¹É¶ØĄķĮŠ·½³ĢĒóµĆm=3£¬m=4£Ø²»ŗĻĢāŅā£¬ÉįČ„£©£¬¢Śµ±”ĻQDB=90”揱£¬øł¾Ż¹“¹É¶ØĄķĮŠ·½³ĢĒóµĆm=8£¬m=©1£¬ÓŚŹĒµĆµ½½įĀŪ£®
£©£¬·ÖĮ½ÖÖĒéæö£ŗ¢Łµ±”ĻQBD=90”揱£¬øł¾Ż¹“¹É¶ØĄķĮŠ·½³ĢĒóµĆm=3£¬m=4£Ø²»ŗĻĢāŅā£¬ÉįČ„£©£¬¢Śµ±”ĻQDB=90”揱£¬øł¾Ż¹“¹É¶ØĄķĮŠ·½³ĢĒóµĆm=8£¬m=©1£¬ÓŚŹĒµĆµ½½įĀŪ£®
ŹŌĢā½āĪö£ŗ£Ø1£©”ßĮīx=0µĆ£»y=2£¬”ąC£Ø0£¬2£©£®
”ßĮīy=0µĆ£ŗ![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() £¬
£¬![]() £¬”ąA£Ø©1£¬0£©£¬B£Ø4£¬0£©£®
£¬”ąA£Ø©1£¬0£©£¬B£Ø4£¬0£©£®
£Ø2£©”ßµćCÓėµćD¹ŲÓŚxÖį¶Ō³Ę£¬”ąD£Ø0£¬©2£©£®
ÉčÖ±ĻßBDµÄ½āĪöŹ½ĪŖy=kx©2£®
”ß½«£Ø4£¬0£©“śČėµĆ£ŗ4k©2=0£¬”ąk=![]() £¬”ąÖ±ĻßBDµÄ½āĪöŹ½ĪŖ
£¬”ąÖ±ĻßBDµÄ½āĪöŹ½ĪŖ![]() £®
£®
£Ø3£©ČēĶ¼1ĖłŹ¾£ŗ
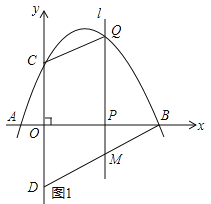
”ßQM”ĪDC£¬”ąµ±QM=CDŹ±£¬ĖıߊĪCQMDŹĒĘ½ŠŠĖıߊĪ£®
ÉčµćQµÄ×ų±źĪŖ£Øm£¬![]() £©£¬ŌņM£Øm£¬
£©£¬ŌņM£Øm£¬![]() £©£¬”ą
£©£¬”ą![]() £¬½āµĆ£ŗm=2£¬m=0£Ø²»ŗĻĢāŅā£¬ÉįČ„£©£¬”ąµ±m=2Ź±£¬ĖıߊĪCQMDŹĒĘ½ŠŠĖıߊĪ£»
£¬½āµĆ£ŗm=2£¬m=0£Ø²»ŗĻĢāŅā£¬ÉįČ„£©£¬”ąµ±m=2Ź±£¬ĖıߊĪCQMDŹĒĘ½ŠŠĖıߊĪ£»
£Ø4£©“ęŌŚ£¬ÉčµćQµÄ×ų±źĪŖ£Øm£¬![]() £©£¬”ß”÷BDQŹĒŅŌBDĪŖÖ±½Ē±ßµÄÖ±½ĒČż½ĒŠĪ£¬”ą·ÖĮ½ÖÖĒéæöĢÖĀŪ£ŗ
£©£¬”ß”÷BDQŹĒŅŌBDĪŖÖ±½Ē±ßµÄÖ±½ĒČż½ĒŠĪ£¬”ą·ÖĮ½ÖÖĒéæöĢÖĀŪ£ŗ
¢Łµ±”ĻQBD=90”揱£¬Óɹ“¹É¶ØĄķµĆ£ŗ![]() £¬¼“
£¬¼“![]() £¬½āµĆ£ŗm=3£¬m=4£Ø²»ŗĻĢāŅā£¬ÉįČ„£©£¬”ąQ£Ø3£¬2£©£»
£¬½āµĆ£ŗm=3£¬m=4£Ø²»ŗĻĢāŅā£¬ÉįČ„£©£¬”ąQ£Ø3£¬2£©£»
¢Śµ±”ĻQDB=90”揱£¬Óɹ“¹É¶ØĄķµĆ£ŗ![]() £¬¼“
£¬¼“![]() £¬½āµĆ£ŗm=8£¬m=©1£¬”ąQ£Ø8£¬©18£©£¬£Ø©1£¬0£©£»
£¬½āµĆ£ŗm=8£¬m=©1£¬”ąQ£Ø8£¬©18£©£¬£Ø©1£¬0£©£»
×ŪÉĻĖłŹö£ŗµćQµÄ×ų±źĪŖ£Ø3£¬2£©£¬£Ø8£¬©18£©£¬£Ø©1£¬0£©£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼ŖĻ鳬ŹŠ×¼±ø¹ŗ½ų¼×”¢ŅŅĮ½ÖÖĀĢÉ«“ü×°Ź³Ę·¹²800“ü£®¼×”¢ŅŅĮ½ÖÖĀĢÉ«“ü×°Ź³Ę·µÄ½ų¼ŪŗĶŹŪ¼ŪČē±ķ£®ŅŃÖŖ£ŗÓĆ2000ŌŖ¹ŗ½ų¼×ÖÖ“ü×°Ź³Ę·µÄŹżĮæÓėÓĆ1600ŌŖ¹ŗ½ųŅŅÖÖ“ü×°Ź³Ę·µÄŹżĮæĻąĶ¬£®
¼× | ŅŅ | |
½ų¼Ū£ØŌŖ/“ü£© | m | m©2 |
ŹŪ¼Ū£ØŌŖ/“ü£© | 20 | 13 |
£Ø1£©ĒómµÄÖµ£»
£Ø2£©¼ŁČē¹ŗ½ųµÄ¼×”¢ŅŅĮ½ÖÖĀĢÉ«“ü×°Ź³Ę·Č«²æĀō³ö£¬Ėł»ń×ÜĄūČó²»ÉŁÓŚ5200ŌŖ£¬ĒŅ²»³¬¹ż5280ŌŖ£¬ĪŹøĆ³¬ŹŠÓŠ¼øÖÖ½ų»õ·½°ø£æ£ØĄūČó£½ŹŪ¼Ū©½ų¼Ū£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy=ax2+bx+c(a”Ł0)µÄ¶Ō³ĘÖįĪŖÖ±Ļßx=1£¬Óė![]() ÖįµÄŅ»øö½»µć×ų±źĪŖ(£1,0)£¬Ęä²æ·ÖĶ¼ĻóČēĶ¼ĖłŹ¾£¬ĻĀĮŠ½įĀŪ£ŗ
ÖįµÄŅ»øö½»µć×ų±źĪŖ(£1,0)£¬Ęä²æ·ÖĶ¼ĻóČēĶ¼ĖłŹ¾£¬ĻĀĮŠ½įĀŪ£ŗ
¢Ł 4ac<b2£»¢Ś ·½³Ģax2+bx+c=0µÄĮ½øöøłŹĒ![]() £»¢Ū 3a+c>0£»¢Ü µ±y>0Ź±£¬xµÄȔֵ·¶Ī§ŹĒ-1”Üx<3£»¢Ż µ±x<0Ź±£¬yĖęxŌö“ó¶ųŌö“ó£»
£»¢Ū 3a+c>0£»¢Ü µ±y>0Ź±£¬xµÄȔֵ·¶Ī§ŹĒ-1”Üx<3£»¢Ż µ±x<0Ź±£¬yĖęxŌö“ó¶ųŌö“ó£»
ĘäÖŠ½įĀŪÕżČ·ÓŠ__________.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻACB=90”ć£¬”ĻB=60”ć£¬BC=2£¬”ĻA”äB”äC”äæÉŅŌÓÉ”÷ABCČʵćCĖ³Ź±ÕėŠż×ŖµĆµ½£¬ĘäÖŠµćA”äÓėµćAŹĒ¶ŌÓ¦µć£¬µćB”äÓėµćBŹĒ¶ŌÓ¦µć£¬Į¬½ÓAB”䣬ĒŅA”¢B”䔢A”äŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬ŌņAA”äµÄ³¤ĪŖ£Ø””””£©

A. 4![]() B. 6 C. 3
B. 6 C. 3![]() D. 3
D. 3
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø±¾Š”Ģā6·Ö£©ĪŖĮĖ²Ī¼ÓÖŠæ¼ĢåÓż²āŹŌ£¬¼×£¬ŅŅ£¬±ūČżĪ»Ķ¬Ń§½ųŠŠ×ćĒņ“«ĒņѵĮ·”£Ēņ“ÓŅ»øöČĖ
½ÅĻĀĖ껜“«µ½ĮķŅ»øöČĖ½ÅĻĀ£¬ĒŅĆæĪ»“«ĒņČĖ“«ĒņøųĘäÓąĮ½ČĖµÄ»ś»įŹĒ¾łµČµÄ£¬Óɼ×æŖŹ¼“«Ēņ£¬¹²“«Čż“Ī”£
£Ø1£©ĒóĒėÓĆŹ÷דĶ¼ĮŠ¾Ł³öČż“Ī“«ĒņµÄĖłÓŠæÉÄÜĒéæö£»
£Ø2£©“«ĒņČż“Īŗó£¬Ēņ»Ųµ½¼×½ÅĻĀµÄøÅĀŹ£»
£Ø3£©Čż“Ī“«Ēņŗó£¬Ēņ»Ųµ½¼×½ÅĻĀµÄøÅĀŹ“ó»¹ŹĒ“«µ½ŅŅ½ÅĻĀµÄøÅĀŹ“ó£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¹ŲÓŚxµÄ·½³Ģ£Øk©1£©x2+£Ø2k©3£©x+k+1=0ÓŠĮ½øö²»ĻąµČµÄŹµŹżøłx1£¬x2£®
£Ø1£©ĒókµÄȔֵ·¶Ī§£»
£Ø2£©ŹĒ·ń“ęŌŚŹµŹżk£¬Ź¹·½³ĢµÄĮ½ŹµŹżøł»„ĪŖĻą·“Źż£æČē¹ū“ęŌŚ£¬Ēó³ökµÄÖµ£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¹śĒģ½ŚĘŚ¼ä£¬Ä³ĪľߵźĘ½¾łĆæĢģæÉĀō³ö300ÕÅŗŲæØ£¬Āō³ö1ÕÅŗŲæØµÄĄūČóŹĒ1ŌŖ.¾µ÷²é·¢ĻÖ£¬ĮćŹŪµ„¼ŪĆæ½µ0.1ŌŖ£¬ĆæĢģæɶąĀō³ö100ÕÅŗŲæØ.ĪŖĮĖŹ¹ĆæĢģ»ńČ”µÄĄūČóøü¶ą£¬øƵź¾ö¶Ø°ŃĮćŹŪµ„¼ŪĻĀ½µ![]() ŌŖ.
ŌŖ.
£Ø1£©ĮćŹŪµ„¼ŪĻĀ½µ![]() ŌŖŗó£¬øƵźĘ½¾łĆæĢģæÉĀō³ö___________ÕÅŗŲæØ£¬ĆæÕÅŗŲæØµÄĄūČóĪŖ___________ŌŖ£»£ØÓĆŗ¬
ŌŖŗó£¬øƵźĘ½¾łĆæĢģæÉĀō³ö___________ÕÅŗŲæØ£¬ĆæÕÅŗŲæØµÄĄūČóĪŖ___________ŌŖ£»£ØÓĆŗ¬![]() µÄŹ½×Ó±ķŹ¾£©
µÄŹ½×Ó±ķŹ¾£©
£Ø2£©ŌŚ²»æ¼ĀĒĘäĖūŅņĖŲµÄĢõ¼žĻĀ£¬øƵźĻ£ĶūĆæĢģĀōŗŲæØ»ńµĆµÄĄūČóŹĒ420ŌŖ£¬²¢ĒŅÄÜĀō³öøü¶ąµÄŗŲæØÓ®µĆŹŠ³”£¬![]() Ó¦¶ØĪŖ¶ąÉŁ£æ
Ó¦¶ØĪŖ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ £Ø2013ÄźĖÄ“ØÄĻ³ä3·Ö£© ČēĶ¼1£¬µćEĪŖ¾ŲŠĪABCD±ßADÉĻŅ»µć£¬µćP£¬µćQĶ¬Ź±“ÓµćB³ö·¢£¬µćPŃŲBE”śED”śDC ŌĖ¶Æµ½µćCĶ£Ö¹£¬µćQŃŲBCŌĖ¶Æµ½µćCĶ£Ö¹£¬ĖüĆĒŌĖ¶ÆµÄĖŁ¶Č¶¼ŹĒ1cm/s£¬ÉčP£¬Q³ö·¢tĆėŹ±£¬”÷BPQµÄĆ껿ĪŖycm£¬ŅŃÖŖyÓėtµÄŗÆŹż¹ŲĻµµÄĶ¼ŠĪČēĶ¼2£ØĒśĻßOMĪŖÅ×ĪļĻßµÄŅ»²æ·Ö£©£¬ŌņĻĀĮŠ½įĀŪ£ŗ¢ŁAD=BE=5cm£»¢Śµ±0£¼t”Ü5Ź±£¬![]() £»¢ŪÖ±ĻßNHµÄ½āĪöŹ½ĪŖ
£»¢ŪÖ±ĻßNHµÄ½āĪöŹ½ĪŖ![]() £»¢ÜČō”÷ABEÓė”÷QBPĻąĖĘ£¬Ōņt=
£»¢ÜČō”÷ABEÓė”÷QBPĻąĖĘ£¬Ōņt=![]() Ćė”£ĘäÖŠÕżČ·µÄ½įĀŪøöŹżĪŖ”¾ ”æ
Ćė”£ĘäÖŠÕżČ·µÄ½įĀŪøöŹżĪŖ”¾ ”æ

A. 4 B. 3 C. 2 D. 1
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃO µÄÖ±¾¶£¬CDŹĒ”ŃOµÄŅ»ĢõĻŅ£¬ĒŅCD”ĶABÓŚµćE£®

£Ø1£©ĒóÖ¤£ŗ”ĻBCO=”ĻD£»
£Ø2£©ČōCD=![]() £¬AE=2£¬Ēó”ŃOµÄ°ė¾¶£®
£¬AE=2£¬Ēó”ŃOµÄ°ė¾¶£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com