
【题目】如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且ADAO=AMAP.
(1)连接OP,证明:△ADM∽△APO;
(2)证明:PD是ΘO的切线;
(3)若AD=24,AM=MC,求![]() 的值.
的值.
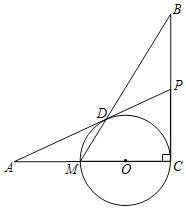
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)根据两边成比例夹角相等两三角形相似证明即可;
(2)通过证明OD⊥PA即可;
(3)连接CD,由(1)可知:PC=PD,由AM=MC,推出AM=2MO=2R,在Rt△AOD中,OD2+AD2=OA2,可得R2+242=9R2,推出R=6![]() ,推出OD=6
,推出OD=6![]() ,MC=12
,MC=12![]() ,由
,由![]() =
=![]() =
=![]() ,可得DP=12,再利用相似三角形的性质求出MD即可解决问题.
,可得DP=12,再利用相似三角形的性质求出MD即可解决问题.
(1)证明:连接OD、OP、CD.
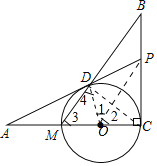
∵ADAO=AMAP,
∴![]() =
=![]() ,∠A=∠A,
,∠A=∠A,
∴△ADM∽△APO.
(2)∵△ADM∽△APO,
∴∠ADM=∠APO,
∴MD∥PO,
∴∠1=∠4,∠2=∠3,
∵OD=OM,
∴∠3=∠4,
∴∠1=∠2,
∵OP=OP,OD=OC,
∴△ODP≌△OCP,
∴∠ODP=∠OCP,
∵BC⊥AC,
∴∠OCP=90°,
∴OD⊥AP,
∴PD是⊙O的切线.
(3)连接CD.由(1)可知:PC=PD,
∵AM=MC,
∴AM=2MO=2R,
在Rt△AOD中,OD2+AD2=OA2,
∴R2+242=9R2,
∴R=6![]() ,
,
∴OD=6![]() ,MC=12
,MC=12![]() ,
,
∵![]() =
=![]() =
=![]() ,
,
∴DP=12,
∵O是MC的中点,
∴![]() =
=![]() =
=![]() ,
,
∴点P是BC的中点,
∴BP=CP=DP=12,
∵MC是⊙O的直径,
∴∠BDC=∠CDM=90°,
在Rt△BCM中,∵BC=2DP=24,MC=12![]() ,
,
∴BM=12![]() ,
,
∵△BCM∽△CDM,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴MD=4![]() ,
,
∴![]() =
=![]() =
=![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】盒中有x枚黑棋和y枚白棋,这些棋除颜色外无其他差别.
(1)从盒中随机取出一枚棋子,如果它是黑棋的概率是![]() ,写出表示x和y关系的表达式.
,写出表示x和y关系的表达式.
(2)往盒中再放进10枚黑棋,取得黑棋的概率变为![]() ,求x和y的值.
,求x和y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】胜利中学从全校学生中随机选取一部分学生,对他们每周上网的时间t进行调查,调查情况分为:![]() 小时;
小时;![]() 小时
小时![]() 小时;
小时;![]() 小时
小时![]() 小时;
小时;![]() 小时四种,并将统计结果制成了如下两幅不完整的统计图,请根据图中信息解答下列问题:
小时四种,并将统计结果制成了如下两幅不完整的统计图,请根据图中信息解答下列问题:
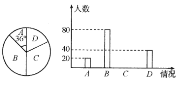
![]() 求参加调查的学生的人数;
求参加调查的学生的人数;
![]() 求扇形图中
求扇形图中![]() 组扇形的圆心角度数,并通过计算补全条形统计图;
组扇形的圆心角度数,并通过计算补全条形统计图;
![]() 在所调查的学生中,随机选取一名学生,求他每周上网时间大于
在所调查的学生中,随机选取一名学生,求他每周上网时间大于![]() 小时的概率.
小时的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象过原点,与x轴的另一个交点为
的图象过原点,与x轴的另一个交点为![]()
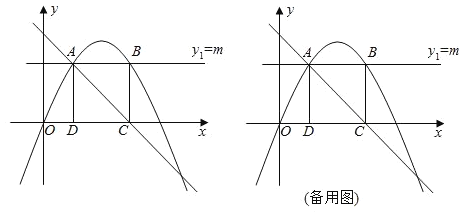
(1)求该二次函数的解析式;
(2)在x轴上方作x轴的平行线![]() ,交二次函数图象于A、B两点,过A、B两点分别作x轴的垂线,垂足分别为点D、点C.当矩形ABCD为正方形时,求m的值;
,交二次函数图象于A、B两点,过A、B两点分别作x轴的垂线,垂足分别为点D、点C.当矩形ABCD为正方形时,求m的值;
(3)在(2)的条件下,动点P从点A出发沿射线AB以每秒1个单位长度匀速运动,同时动点Q以相同的速度从点A出发沿线段AD匀速运动,到达点D时立即原速返回,当动点Q返回到点A时,P、Q两点同时停止运动,设运动时间为t秒(![]() ).过点P向x轴作垂线,交抛物线于点E,交直线AC于点F,问:以A、E、F、Q四点为顶点构成的四边形能否是平行四边形.若能,请求出t的值;若不能,请说明理由.
).过点P向x轴作垂线,交抛物线于点E,交直线AC于点F,问:以A、E、F、Q四点为顶点构成的四边形能否是平行四边形.若能,请求出t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。

(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,我们将横、纵坐标都是整数的点称为“整点”.若抛物线y=ax2﹣2ax+a+3与x轴围成的区域内(不包括抛物线和x轴上的点)恰好有8个“整点”,则a的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
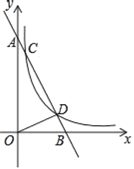
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,直线AB与反比例函数y=![]() (m>0)在第一象限的图象交于点C、点D,其中点C的坐标为(1,8),点D的坐标为(4,n).
(m>0)在第一象限的图象交于点C、点D,其中点C的坐标为(1,8),点D的坐标为(4,n).
(1)分别求m、n的值;
(2)连接OD,求△ADO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着天气的逐渐炎热(如图1),遮阳伞在我们的日常生活中随处可见如图2所示,遮阳伞立柱OA垂直于地面,当将遮阳伞撑开至OD位置时,测得∠ODB=45°,当将遮阳伞撑开至OE位置时,测得∠OEC=30°,且此时遮阳伞边沿上升的竖直高度BC为20cm,求若当遮阳伞撑开至OE位置时伞下阴凉面积最大,求此时伞下半径EC的长.(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com