
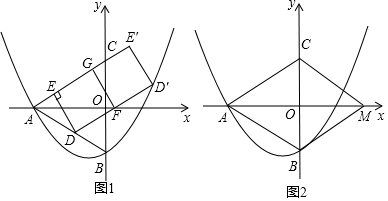
���� ��1����A��B��������������ߵĽ���ʽ��⼴�ɣ�
��2���ɵȱ������ε����ʿ�֪��BAC=60�㣬��������������Ǻ���ֵ�ɵõ�AE=t��DE=$\sqrt{3}$t��AF=2$\sqrt{3}$t��Ȼ����֤��AD=DF=2t������D����D��H��x�����H��������������õ�D������꣬���D���������������ߵĽ���ʽ��⼴�ɣ�
��3����0��t��$\frac{4}{3}$ʱ��S=ED•DF����$\frac{4}{3}$��t��2ʱ��S=����DEGF�����-��CGN�������
��� �⣺��1����A��-2$\sqrt{3}$��0����B��0��-2�����������ߵĽ���ʽ�ã�$\left\{\begin{array}{l}{c=-2}\\{\frac{1}{3}��12-2\sqrt{3}b+c=0}\end{array}\right.$����ã�$\left\{\begin{array}{l}{c=-2}\\{b=\frac{\sqrt{3}}{3}}\end{array}\right.$��
�������ߵĽ���ʽΪy=$\frac{1}{3}$x2+$\frac{\sqrt{3}}{3}$x-2��
��2��A��-2$\sqrt{3}$��0����B��0��-2����
��OA=2$\sqrt{3}$��OB=2��
��AD=2t����DEA=90�㣬��BAC=60�㣬
��AE=t��DE=$\sqrt{3}$t��
�ߡ�ABCΪ�ȱ������Σ�
���BAC=60�㣮
��AO��BC��
���CAO=��BAO=30�㣮
���ı���DEGFΪ���Σ�
��DF��AC��GF=DE=$\sqrt{3}$t��
���DFA=��CAO=30�㣬
��AF=2GF=2$\sqrt{3}$t��
���DFA=��BAO=30�㣮
��DF=AD=2t��
����D����D��H��x�����H��
�ߡ�D��FH=��AFD=30�㣬
��D��H=$\frac{1}{2}$D��F=t��FH=$\sqrt{3}$D��H=$\sqrt{3}$t��
��AH=AF+FH=3$\sqrt{3}$t��
��OH=AH-AO=3$\sqrt{3}$t-2$\sqrt{3}$��
��D�䣨3$\sqrt{3}$t-2$\sqrt{3}$��t����
�ѵ�D�䣨3$\sqrt{3}$t-2$\sqrt{3}$��t������y=$\frac{1}{3}$x2+$\frac{\sqrt{3}}{3}$x-2�ã�t=$\frac{1}{3}$��3$\sqrt{3}$t-2$\sqrt{3}$��2+$\frac{\sqrt{3}}{3}$��3$\sqrt{3}$t-2$\sqrt{3}$��-2�������ã�9t2-10t=0��
���t=$\frac{10}{9}$��t=0����ȥ����
��D�䣨$\frac{4\sqrt{3}}{3}$��$\frac{10}{9}$����
��3���ɣ�2����֪��DE=$\sqrt{3}$t��DF=2t��AE=t��
��ͼ2��ʾ����AE+EG��ACʱ����t+2t��4����ã�t��$\frac{4}{3}$��
�൱0��t��$\frac{4}{3}$ʱ��S=ED•DF=2$\sqrt{3}$t2��
��$\frac{4}{3}$��t��2ʱ����ͼ3��ʾ��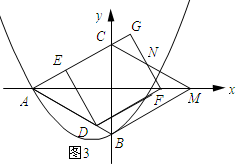
��CG=AG-AC��
��CG=3t-4��
��GN=3$\sqrt{3}$t-4$\sqrt{3}$��
��S=ED•DF-$\frac{1}{2}$CG•GN=2$\sqrt{3}$t2-$\frac{1}{2}$��3t-4����$\sqrt{3}$��3t-4��=-$\frac{5\sqrt{3}}{2}$t2+12$\sqrt{3}$t-8$\sqrt{3}$��
����������S��t�ĺ�����ϵʽΪS=$\left\{\begin{array}{l}{2\sqrt{3}{t}^{2}��0��t��\frac{4}{3}��}\\{-\frac{5\sqrt{3}}{2}{t}^{2}+12\sqrt{3}t-8\sqrt{3}��\frac{4}{3}��t��2��}\end{array}\right.$��
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ��������κ����Ľ���ʽ���ȱ������ε����ʣ�����������Ǻ���ֵ����õ�D�䣨�ú�t��ʽ�ӱ�ʾ���ǽ�������⣨2���Ĺؼ����������⻭�����������ͼ���ǽ�����⣨3���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 13 | B�� | 24 | C�� | 31 | D�� | 42 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪?ABCD�������S����������?ABCD�����е㹹�ɵڶ���ƽ���ı���?EFGH�����������ӵڶ���ƽ���ı��θ����е㹹�ɵ�����ƽ���ı��Σ����Դ����ƣ����109��ƽ���ı��ε����Ϊ$\frac{1}{{2}^{108}}$S��
��ͼ����֪?ABCD�������S����������?ABCD�����е㹹�ɵڶ���ƽ���ı���?EFGH�����������ӵڶ���ƽ���ı��θ����е㹹�ɵ�����ƽ���ı��Σ����Դ����ƣ����109��ƽ���ı��ε����Ϊ$\frac{1}{{2}^{108}}$S���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢ڢۢ� | B�� | �٢� | C�� | �ڢ� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
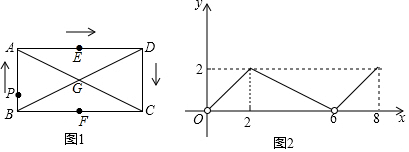
| A�� | ��C | B�� | ��E | C�� | ��F | D�� | ��G |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com