
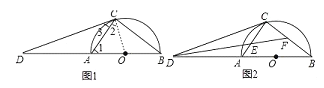
【题目】如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;
①求tan∠CFE的值;
②若AC=3,BC=4,求CE的长.

【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OC,根据切线的性质、直径所对的圆周角是直角及等角的余角相等即可证明结论.
(2)①由∠CEF=∠ECD+∠CDE,∠CFE=∠B+∠FDB,∠CDE=∠FDB,∠ECD=∠B,即可得∠CEF=∠CF,再由∠ECF=90°,可得∠CEF=∠CFE=45°,即可得结论.
②由勾股定理可求得AB=5,根据已知易证△DCA∽△DBC,得![]() ,设DC=3k,DB=4k,由CD2=DADB,得9k2=(4k﹣5)4k,由此求出DC,DB,再由△DCE∽△DBF,得
,设DC=3k,DB=4k,由CD2=DADB,得9k2=(4k﹣5)4k,由此求出DC,DB,再由△DCE∽△DBF,得![]() ,设EC=CF=x,列出方程即可解决问题.
,设EC=CF=x,列出方程即可解决问题.
试题解析:(1)证明:如图1中,连接OC.
∵OA=OC,
∴∠1=∠2,
∵CD是⊙O切线,
∴OC⊥CD,
∴∠DCO=90°,
∴∠3+∠2=90°,
∵AB是直径,
∴∠1+∠B=90°,
∴∠3=∠B.
(2)解:①∵∠CEF=∠ECD+∠CDE,∠CFE=∠B+∠FDB,
∵∠CDE=∠FDB,∠ECD=∠B,
∴∠CEF=∠CFE,∵∠ECF=90°,
∴∠CEF=∠CFE=45°,
∴tan∠CFE=tan45°=1.
②在RT△ABC中,∵AC=3,BC=4,
由勾股定理得AB=5,
∵∠CDA=∠BDC,∠DCA=∠B,
∴△DCA∽△DBC,
∴![]() ,设DC=3k,DB=4k,
,设DC=3k,DB=4k,
∵CD2=DADB,
∴9k2=(4k﹣5)4k,
∴k=![]() ,
,
∴CD=![]() ,DB=
,DB=![]() ,
,
∵∠CDE=∠BDF,∠DCE=∠B,
∴△DCE∽△DBF,
∴![]() ,设EC=CF=x,
,设EC=CF=x,
∴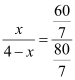 ,
,
∴x=![]() .
.
∴CE=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知关于x的二次函数y=ax2+bx+c的图象经过点(﹣2,y1),(﹣1,y2),(1,0),且y1<0<y2,对于以下结论:①abc>0;②a+3b+2c≤0;③对于自变量x的任意一个取值,都有![]() x2+x≥﹣
x2+x≥﹣![]() ;④在﹣2<x<﹣1中存在一个实数x0,使得x0=﹣
;④在﹣2<x<﹣1中存在一个实数x0,使得x0=﹣![]() ,其中结论错误的是 (只填写序号).
,其中结论错误的是 (只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高科技创新意识,我市某中学在“2016年科技节”活动中举行科技比赛,包括“航模”、“机器人”、“环保”、“建模”四个类别(每个学生只能参加一个类别的比赛),各类别参赛人数统计如图:

请根据以上信息,解答下列问题:
(1)全体参赛的学生共有 人,“建模”在扇形统计图中的圆心角是 °;
(2)将条形统计图补充完整;
(3)在比赛结果中,获得“环保”类一等奖的学生为1名男生和2名女生,获得“建模”类一等奖的学生为1名男生和1名女生,现从这两类获得一等奖的学生中各随机选取1名学生参加市级“环保建模”考察活动,问选取的两人中恰为1男生1女生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数表达式是y = 60x-1.5x2,该型号飞机着陆后需滑行 m才能停下来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若直线l与直线y=2x﹣3关于y轴对称,则直线l的解析式是( )
A. y=﹣2x+3B. y=﹣2x﹣3C. y=2x+3D. y=2x﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O1与⊙O2的圆心距O1O2=6cm,且两圆的半径满足一元二次方程x2-6x+8=0,则两圆的位置关系为 ( )
A. 外切 B. 内切 C. 外离 D. 相交
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com