练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．如图，AB∥CD，FE⊥DB，垂足为E，∠1=50°，则∠2的度数是（　　）
    A．60°B．50°C．40°D．30°

    分析 根据直角三角形的两锐角互余，求出∠D=40°，再根据平行线的性质即可解答．

    解答 解：如图所示，
    ∵FE⊥BD，
    ∴∠FED=90°，
    ∴∠1+∠D=90°，
    ∵∠1=50°，
    ∴∠D=40°，
    ∵AB∥CD，
    ∴∠2=∠D=40°．
    故选C．

    点评 本题主要考查平行线的性质、垂线及直角三角形的性质，解决此题时，根据直角三角形的性质求出∠D的度数是解决此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    11．已知直角三角形ABC中，点D为斜边BC的中点，AC=4，BC=8，直角EDF的两边分别与直线AC，直线AB交于点E和点F，BF=7，则AE的长为7$\sqrt{3}$-4或7$\sqrt{3}$+4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，△ABC中，∠C=90°，AC=3cm，BC=6cm，动点P从点B出发以2cm/s的速度向点C移动，动点Q从C出发以1cm/s的速度向点A移动，如果动点P、Q同时出发，要使△CBA与C、P、Q三点构成的三角形相似，求所需要的时间是多少秒？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．方程组$\left\{\begin{array}{l}{x+y=1}\\{2x+y=5}\end{array}\right.$的解为（　　）
    A．$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$B．$\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$C．$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$D．$\left\{\begin{array}{l}{x=4}\\{y=-3}\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．一个样本的50个数据分别落在5个小组内，第1、2、3、4组的数据的个数分别2、8、15、5，则第5组的频率为0.4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

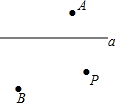    19．如图，平面上有直线a及直线a外的三点A、B、P．
    （1）过点P画一条直线m，使得m∥a；
    （2）过B作BH⊥直线m，并延长BH至B′，使得BB′为直线a、m之间的距离；
    （3）若直线a、m表示一条河的两岸，现要在这条河上建一座桥（桥与河岸垂直），使得从村庄A经桥过河到村庄B的路程最短，试问桥应建在何处？画出示意图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．某农民带了若干千克土豆进城出售，为了方便，他带了一些零用钱备用，他先按市场价卖出一些后，又降价卖，卖出土豆千克数x与他手中持有的钱数y（含备用零钱）的关系如图所示．结合图象回答下列问题：
    （1）该农民自带的零钱是多少？
    （2）降价前土豆的单价是多少？
    （3）降价后他按每千克0.4元将剩余下的土豆售完，这时他手中的钱（含备用零钱）是26元，问他一共带了多少千克土豆？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．【试题背景】已知：l∥m∥n∥k，平行线l与m、m与n、n与k之间的距离分别为d1、d2、d3，且d1=d3=1，d2=2．我们把四个顶点分别在l、m、n、k这四条平行线上的四边形称为“绣湖四边形”．
    【探究1】（1）如图1，正方形ABCD为“绣湖四边形”，BE⊥l于点E，BE的反向延长线交直线k于点F．求正方形ABCD的边长．
    【探究2】（2）矩形ABCD为“绣湖四边形”，其长：宽=2：1，则矩形ABCD的宽为．（直接写出结果即可）
    【探究3】（3）如图2，菱形ABCD为“绣湖四边形”且∠ADC=60°，△AEF是等边三角形，AE⊥k于点E，∠AFD=90°，直线DF分别交直线l、k于点G、M．求证：EC=DF．
    【拓 展】（4）如图3，l∥k，等边三角形ABC的顶点A、B分别落在直线l、k上，AB⊥k于点B，且AB=4，∠ACD=90°，直线CD分别交直线l、k于点G、M，点D、E分别是线段GM、BM上的动点，且始终保持AD=AE，DH⊥l于点H．猜想：DH在什么范围内，BC∥DE？并说明此时BC∥DE的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

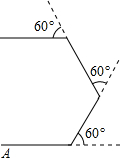    4．如图，小明从点A出发，沿直线前进8m后向左转60°，再沿直线前进8m，又向左转60°…照这样走下去，小明第一次回到出发点A，一共走了48米．

    查看答案和解析>>

    同步练习册答案