
【题目】如图,己知抛物线经过点A(l, 0),B(一3,0),C(0,3)三点.
(1)求抛物线的解析式;
(2)在x轴下方的抛物线上,是否存在点M,使得![]() ?若存在求出M点的坐标;若不存在,请说明理由;
?若存在求出M点的坐标;若不存在,请说明理由;
(3)点P是位于直线BC上方的抛物线上的一个动点,是否存在点P,使![]() 的面积最大?若存在,求出P的坐标及
的面积最大?若存在,求出P的坐标及![]() 的最大值:若不存在,说明理由.
的最大值:若不存在,说明理由.

【答案】(1) ![]()
(2)M点的坐标为:(-4,-5),(2,-5).
(3)当![]() 时,
时, ![]() 最大,最大值为
最大,最大值为![]() 。
。
【解析】试题分析:(1)由抛物线经过三点,可设抛物线的解析式为![]() ,将A、B、C三点带入方程即可求得a、b、c的值;
,将A、B、C三点带入方程即可求得a、b、c的值;
(2)设存在点M(a,b),由题意可知, ![]() 以AB=4为底,则高为OC=3,因此
以AB=4为底,则高为OC=3,因此![]() =10 ,又在
=10 ,又在![]() 中,以AB=4为底,则高为
中,以AB=4为底,则高为![]() ,所以
,所以![]() =
=![]() ,因为M点在x轴的下方,故b<0,因此b=-5,又因为M在抛物线上,所以满足抛物线方程。代入得:
,因为M点在x轴的下方,故b<0,因此b=-5,又因为M在抛物线上,所以满足抛物线方程。代入得: ![]() ,解得,
,解得, ![]() ,即可得到M点的坐标;
,即可得到M点的坐标;
(3)连接PC、PB,过P作PR⊥x轴,交BC于点Q,可知当PQ有最大值时, ![]() 有最大值,由待定系数法求得直线BC的解析式,设出点P的坐标,进而得出Q点坐标,表示出 PQ的长度,求出最大值,即可解决问题.
有最大值,由待定系数法求得直线BC的解析式,设出点P的坐标,进而得出Q点坐标,表示出 PQ的长度,求出最大值,即可解决问题.
试题分析:(1)设抛物线方程为![]() ,
,
将A(l,0),B(-3,0),C(0,3)带入方程得: 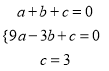 ,
,
解得 ,所以抛物线的解析式为:
,所以抛物线的解析式为: ![]() ;
;
(2)设存在点M(a,b),由题意可知, ![]() =
=![]() ×4×3=6,
×4×3=6,
∴![]() =
=![]() ,
, ![]() =5,
=5,
因为M点在x轴的下方,故b<0,因此b=-5,
又因为M在抛物线上,所以满足抛物线方程,
代入得: ![]() ,解得,
,解得, ![]() ,
,
所以M点的坐标为:(-4,-5),(2,-5).
(3)如图:
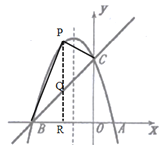
连接PC、PB,过P作PR⊥x轴,交BC于点Q,
设直线BC的解析式为:y=kx+m,把B(-3,0),C(0,3)代入,
则![]() ,
,
解得: ![]() ,
,
则直线BC的解析式是y=x+3.
设点P的坐标为(x, ![]() ),则Q坐标为(x
),则Q坐标为(x![]() ),
),
PQ=![]() =-(x+
=-(x+![]() )2+
)2+![]() ,
,
当x=-![]() 时,PQ有最大值
时,PQ有最大值![]() ,此时
,此时![]() 有最大值为:
有最大值为: ![]() ×
×![]() ×3=
×3=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列四个说法:
①两点之间,直线最短;
②直线外一点与直线上各点连接的所有线段中,垂线段最短;
③连接两点的线段,叫做两点的距离;
④从直线外一点到这条直线的垂线段的长度叫做点到直线的距离.
其中正确的是( )
A.①② B.①③ C.②③ D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB,与y轴交于D点,∠CAO=90°-∠BDO.
(1)求证:AC=BC:
(2)如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长;

(3)如图3,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,当H在FC上移动、点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.
 (图3)
(图3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com