
 图中有四个相邻点围成正方形面积是一个单位面积.在求图中点阵中多边形的面积时,你可以将多边形分割成若干个小正方形和三角形,分别计算面积后相加;或者你可能想到通过剪拼的方法计算.
图中有四个相邻点围成正方形面积是一个单位面积.在求图中点阵中多边形的面积时,你可以将多边形分割成若干个小正方形和三角形,分别计算面积后相加;或者你可能想到通过剪拼的方法计算.| a | $\frac{1}{2}b$ | S | S,a,b之间 的关系式 | |
| ① | ||||
| ② | 4.5 | |||
| … | … | … | … |
分析 (1)割补法求解可得;
(2)根据要求依据割补法作出图形,从而得出点的分布数量可得;
(3)根据图①和图②中点的分布情况与面积间的关系可得S=a+$\frac{1}{2}$b-1.
解答 解:(1)图①中多边形的面积为2×3+$\frac{1}{2}$×3×1+$\frac{1}{2}$×1×2=8.5,
故答案为:8.5;
(2)如图②所示: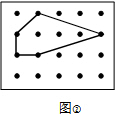
在这个多边形内部的点数为3个,在这个多边形边界上的点数为5个,
故答案为:3,5;
(3)由图①知多边形内部点数a=5,边界上点数b=9,其面积8.5=5+$\frac{1}{2}$×9-1,
图②中多边形内部点数a=3,边界上的点数b=5,其面积4.5=3+$\frac{1}{2}$×5-1,
∴S=a+$\frac{1}{2}$b-1.
点评 本题主要考查图形的变化规律及割补法求图形的面积,根据已知图形得出点的分布情况与面积的关系是解题的关键.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
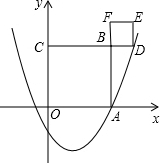 如图,抛物线y=ax2-x-$\frac{3}{2}$与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.求a的值和点E的坐标.
如图,抛物线y=ax2-x-$\frac{3}{2}$与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.求a的值和点E的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
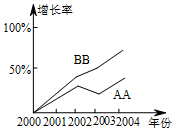 如图,是两种品牌的方便面销售增长率折线统计图,则AA牌方便面2003年的销售量低于2002年的销售量,2002年BB牌方便面的销售量高于AA牌方便面的销售量(填“高于”“低于”“不一定高于”)
如图,是两种品牌的方便面销售增长率折线统计图,则AA牌方便面2003年的销售量低于2002年的销售量,2002年BB牌方便面的销售量高于AA牌方便面的销售量(填“高于”“低于”“不一定高于”)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com