
【题目】如图,AB∥CD∥EF,CD交AF于G,
(1)如图1,若CF平分∠AFE,∠A=70°,求∠C;
(2)如图2,请写出∠A,∠C和∠AFC的数量关系并说明理由.
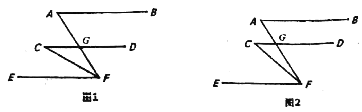
【答案】(1)∠C=35°;(2)∠A=∠C+∠AFC. 理由见解析.
【解析】
(1)由平行线的性质可求出∠AFE=70°,由角平分线的定义可求∠CFE=35°,然后再根据平行线的性质即可求出求∠C;
(1)由AB∥CD,可得∠DGF=∠A,由三角形外角的性质可得∠DGF=∠C+∠AFC,进而可求出∠A,∠C和∠AFC的数量关系.
(1)∵AB∥EF, ∠A=70°,
∴∠AFE=∠A=70°,
∵CF平分∠AFE,
∴∠CFE=![]() ∠AFE=35°.
∠AFE=35°.
∵CD∥EF,
∴∠C=∠CFE=35°;
(2)∵AB∥CD,
∴∠DGF=∠A.
∵∠DGF是△GCF的外角,
∴∠DGF=∠C+∠AFC,
∴∠A=∠C+∠AFC.


科目:初中数学 来源: 题型:
【题目】定义:如果一个数的平方等于![]() ,记为
,记为![]() ,这个数
,这个数![]() 叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为
叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为![]() (
(![]() 为实数),
为实数),![]() 叫这个复数的实部,
叫这个复数的实部, ![]() 叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算: ![]()
(1)填空: ![]() =_________,
=_________, ![]() =____________.
=____________.
(2)填空:①![]() _________; ②
_________; ②![]() _________ .
_________ .
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知, ![]() ,(
,( ![]() 为实数),求
为实数),求![]() 的值.
的值.
(4)试一试:请利用以前学习的有关知识将![]() 化简成
化简成![]() 的形式.
的形式.
(5)解方程:x2 - 2x +4 = 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司经销甲种型号电脑,今年三月份的电脑售价比去年同期每台降价1000元.如果卖出相同数量的电脑,去年的销售额为10万元,那么今年的销售额只有8万元.
(1)今年三月份甲种型号电脑每台的售价为多少元?
(2)为增加收入,电脑公司决定经销乙种型号电脑.已知甲种型号电脑每台的进价为3500元,乙种型号电脑每台的进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种型号的电脑共15台,则有几种进货方案?
(3)如果乙种型号电脑每台的售价为3800元,为打开乙种型号电脑的销路,公司决定每售出一台乙种型号电脑,返还顾客现金![]() 元,要使(2)中所有方案的获利相同,那么
元,要使(2)中所有方案的获利相同,那么![]() 的值应是多少?
的值应是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
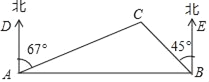
【题目】一艘救生船在码头A接到小岛C处一艘渔船的求救信号,立即出发,沿北偏东67°方向航行10海里到达小岛C处,将人员撤离到码头A张东方向的码头B,测得小岛C位于码头B西北方向,求码头B与小岛C的距离(结果精确到0.1海里).【参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42, ![]() =1.41】
=1.41】
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=4,BC=6,∠ABC=60°,点P为ABCD内一点,点Q在BC边上,则PA+PD+PQ的最小值为( )
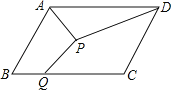
A.![]() B.6+2
B.6+2![]() C.5
C.5![]() D.10
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与点B,C重合),过点C作CN⊥DM交AB于点N,连结OM、ON,MN.下列五个结论:①△CNB≌△DMC;②ON=OM;③ON⊥OM;④若AB=2,则S△OMN的最小值是1;⑤AN2+CM2=MN2.其中正确结论是_____;(只填序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com