练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．点A（-1，y1）和点B（3，y2）在反比例函数y=-$\frac{1}{x}$图象上，则y1与y2的大小关系是（　　）
    A．y1=y2B．y1＞y2C．y1＜y2D．无法确定

    分析 先根据点A（-1，y1）和点B（3，y2）在反比例函数y=-$\frac{1}{x}$图象上，求得y1与y2的值，再比较大小．

    解答 解：∵点A（-1，y1）和点B（3，y2）在反比例函数y=-$\frac{1}{x}$图象上，
    ∴y1=1，y2=$-\frac{1}{3}$，
    ∴y1与y2的大小关系是y1＞y2．
    故选（B）．

    点评 本题主要考查了反比例函数图象上点的坐标特征，解题时注意：反比例函数图象上的点（x，y）的横纵坐标的积是定值k，即xy=k．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    1．下列问题的调查适合用全面调查方式的有（　　）
    ①汽车制造厂检验一批出厂汽车的刹车性能；
    ②了解某班学生的视图情况；
    ③了解我国70岁以上老年人的健康状况；
    ④检验某品牌食品质量是否合格．
    A．4个B．3个C．2个D．1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．如图，9点整时，时针与分针夹角为90°，则下一次时针与分针夹角为90°时，经过了（　　）分钟．
    A．$\frac{90}{11}$B．$\frac{180}{11}$C．$\frac{270}{11}$D．$\frac{360}{11}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．如图，在一个足够大的桌面上，画满了等距的平行线，间距为2厘米，现有一个半径为r厘米的圆形硬币，若事件“将该硬币任意掷于桌面上，硬币压到所画直线”是必然事件，则r的取值可以是2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知在矩形ABCD中，∠ADC的平分线DE与BC边所在的直线交于点E，点P是线段DE上一定点（其中EP＜PD）
    （1）如图1，若点F在CD边上（不与D重合），将∠DPF绕点P逆时针旋转90°后，角的两边PD、PF分别交射线DA于点H、G．
    ①求证：PG=PF；      ②探究：DF、DG、DP之间有怎样的数量关系，并证明你的结论．
    （2）拓展：如图2，若点F在CD的延长线上（不与D重合），过点P作PG⊥PF，交射线DA于点G，你认为（1）中DF、DG、DP之间的数量关系是否仍然成立？若成立，给出证明；若不成立，请写出它们所满足的数量关系式，并说明理由．

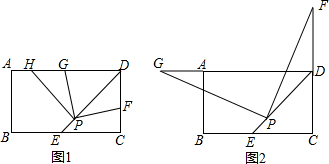
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．将代数式x2-6x+2化为（x+p）2+q的形式为（　　）
    A．（x-3）2+11B．（x+3）2-7C．（x-3）2-7D．（x+3）2+11

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

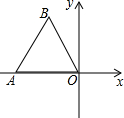    3．如图，点O为平面直角坐标系的原点，点A在x轴上，△OAB是边长为4的等边三角形，以O为旋转中心，将△OAB按顺时针方向旋转60°，得到△OA′B′，那么点A′的坐标为（　　）
    A．（2，2$\sqrt{3}$）B．（-2，4）C．（-2，2$\sqrt{2}$）D．（-2，2$\sqrt{3}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．甲、乙两班各50名同学参加世博会体操表演竞选，经测量并计算得甲、乙两班同学身高的平均数和方差为：$\overline{{x}_{甲}}$=165（cm），$\overline{{x}_{乙}}$=165（cm），S甲2=7.5，S乙2=21.6，世博会组委会从身高整齐美观效果来看，应选甲班参加表演．（填“甲”或“乙”）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知：二次函数y=（a-3）x2-2（a2-6a+10）x+1（a≠3）．
    （1）当a=5，求此二次函数图象的顶点坐标．
    （2）设a为大于4的整数，x为正整数
    ①在括号内填上适当的内容使等式成立
    由题意得抛物线的对称轴
    h=$\frac{-2（{a}^{2}-6a+10）}{2（a-3）}$=$\frac{{a}^{2}-6a+10}{（）}$=$\frac{（）^{2}+1}{a-3}$=a-3+$\frac{（）}{a-3}$
    ②用a的代数式表示h的整数部分，并说明理由．
    ③当二次函数取得最小值时，求正整数x的值．（用a的代数式表示）

    查看答案和解析>>

    同步练习册答案